* 9 квадратчета
Публикувано на 23 април 2013 в раздел Математика.
Следната задача може спокойно да се нарече основополагаща за един цял клас от задачи, които развиват логическото мислене при децата. Подобни често се дават на олимпиади.
Задача: Игрална площадка е разделена на 9 квадратчета, както е показано на фигурата. Във всяко от тях стои по едно дете. По подаден сигнал всяко едно от децата се премества в съседно квадратче. За съседно приемаме квадратче, което има обща страна с текущото. Докажете, че след преместването винаги ще има поне едно квадратче, в което ще се намират две или повече деца.
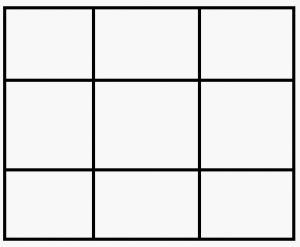
Ако оцветим ъгловите квадратчета в червено, централното в бяло, а останалите в зелено, то можем да разсъждаваме така:
1) С преместването си децата от червените квадратчета ги напускат, но могат да отидат само на зелени,
2) За да се запълнят червените квадратчета, там трябва да отидат децата от зелените, защото това от бялото не може да стигне до червено.
3) Детето от бялото квадратче трябва да го напусне, но може да отиде само на зелено.
4) Следователно, бялото квадратче ще остане празно.
Докажете, че след преместването винаги ще има поне едно квадратче, в което ще се намират две или повече деца.
Това изречение ни навежда на мисълта че ще има нещо с принципа на Дирихле. А пък това че се местят в съседни квадратчета ни навежда на мисълта за шахматно оцветяване. (То тука е малко на принципа „умен съм бил, сетил съм се“, ама като сме решавали и преди такива задачи и ни идва свисше). Та… да се върнем на задачата. Оцветяваме квадратчетата шахматно, като БОО (Без ограничение на общността) горното ляво квадратче е бяло, а горното средно квадратче е черно. Идеята е да се получи нещо такова:
Общо белите квадратчета са 5, а черните – 4. След подаденият сигнал, децата от белите квадратчета скачат в/у черни, а децата върху черните – на бели. Тъй като в начало имаме 5 деца на петте бели квадратчета, след скоковете в/у черните квадратчета ще имаме същите тези 5 деца. (Тези, които са „оригинално“ върху черни ще отидат на бели, а на тяхно място върху черните квадратчета ще дойдат деца, които до сега са били на бели). Или накратко ще имаме 5 деца стъпили върху 4 черни квадратчета. От тук връзката с принципа на Дирихле е очевидна.
Даже можем да отидем по-далеч и да посочим 4 квадратчета, от които поне върху едно ще има поне две деца. (Същите тези черни квадратчета от нашето оцветяване). Въпреки че, ако в условието се искаше да се докаже това по-силно твърдение, то това би било своеобразна подсказка, т.е. задачата би била по-лесна, а не по-трудна. (По мое скромно мнение).
Също така задачата може да се обобщи за произволна мрежа с нечетен брой квадратчета. (разбира се с изключение на 1х1).
Точно така, принцип на Дирихле е.