* Положения на n точки върху окръжност
Публикувано на 17 декември 2010 в раздел Вероятности.
Задача 1: Дадена е окръжност с радиус 1. Избираме три произволни точки A, B и C, които лежат на нея. Каква е вероятността триъгълникът ABC да съдържа центъра на окръжността?
Решение: Всеки две произволни точки върху окръжност я разделят на две дъги - къса и дълга. Без да ограничаваме решенията обозначаваме тези две точки с A и B. Нека късата дъга AB е с дължина "x". Прекарваме лъчи AO и BO, които пресичат окръжността съответно в точки A' и B'. Ако точка C лежи в дъгата A'B', то центъра на окръжността ще бъде вътрешна точка за нея:
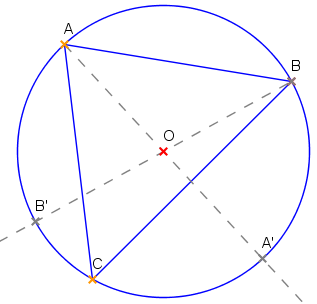
Ако дължината на дъжата AB е x, то и дължината на дъгата A'B' също ще е x. Вероятността точка C да лежи в дъгата A'B' е x/2π. Да но самото "x" може да се мени от 0 до π. Следователно вероятността точка O да лежи вътре в триъгълника е:
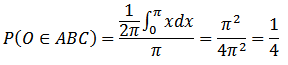
Този резултат никак не е изненадващ. Ако погледнете внимателно ще видите, че ако точка O е вътре в триъгълника, то триъгълника е остроъгълен и обратно - ако е вън от него, то триъгълника е тъпоъгълен. Ние вече знаем вероятността произволен триъгълник в равнината да бъде остроъгълен - тя е 1/4. Оказва се, че решението на задачата не зависи от радиуса на окръжността (което и логично идва от задачата за произволен триъгълник, защото около всеки триъгълник може да се опише окръжност).
Нека разгледаме друга интересна интерпретация на задачата - ако точка C не лежи в дъгата A'B', то се оказва, че точките A, B и C ще лежат в една полуокръжност (B'AB или A'BA). Следователно търсената вероятност от тази задача може да се преформулира така: "Каква е вероятността три точки от окръжност да НЕ лежат в една полуокръжност?". Решението вече го знаем - 1/4
Задача 1'. Каква е вероятността три точки лежащи върху окръжност да се намират в една полуокръжност?
Решение: От Задача 1 знаем, че вероятността трите точки да НЕ лежат в една полуокръжност е 1/4. Следователно търсената вероятност е P=1-1/4 = 3/4. Това естествено съвпада и с вероятността триъгълника да е тъпоъгълен.
Задача 2. Четири точки лежат върху една окръжност. Каква е вероятността четирите точки да лежат в една полуокръжност?
Решение: Тук ще започнем с различен подход. Нека вземем която и да е полуокръжност. Вероятността и четирите точки да попаднат в нея е (1/2)*(1/2)*(1/2)*(1/2)=1/24=1/16.
Сега трябва да отбележим, че всеки четири точки могат да разделят една окръжност на общо 2*4=8 полуокръжности, защото всеки диаметър с край една от точките разделя окръжността на две полуокръжности. Естествено тези 8 полуокръжности се засичат една друга. Така вероятността точките да лежат в някоя от тези 8 полуокръжности е P=8*(1/16)=1/2.
Задача 3. "n" на брой точки лежат върху една окръжност. Каква е вероятността всичките точки да лежат в една полуокръжност?
Решение: Подобно на задача 2. можем да формулираме, че вероятността всички точки да попаднат в произволна окръжност е 1/2n, а възможните полуокръжности са 2n. Следователно вероятността е P=2n/2n.
Нека за всеки случай да проверим дали тази формула работи с предишните задачи:
1 точка: 2/2 = 1
2 точки: 4/4 = 1
3 точки: 6/8 = 3/4
4 точки: 8/16 = 1/2
5 точки: 10/32 = 5/16
и т.н.
Направете проверка с компютърна прорама за частния случай с 5 точки.
Задача 4. Четири точки лежат върху една окръжност. Каква е вероятността центърът на окръжността да лежи вътре в четиригълника, образуван при свързването на всеки две "съседни" точки с отсечка?
Пояснение: Ще казваме, че точката Q е съседна на P, ако не съществува друга точка Q' такава, че хордата PQ' е по-къса от хордата PQ.
Решение: Избираме две съседни точки A и B, които от предишните задачи вече знаем, че определят общо четири полуокръжности, но в комбинация винаги лежат в две засичащи се от тях. Нека късата дъга AB е с дължина x.
Сега нека вземем третата точка C. Тя ще е или по-близо до A или по-близо до B. Отново без да ограничаваме решенията приемаме, че тя е по-близо до B (ако не е, то просто сменяме означенията на точките A и B и разглеждаме дъгата в обратна посока). Нека късата дъга BC е с дължина y.
Построяваме лъчите AO, BO и CO, които пресичат окръжността в точки A', B' и C'. Лесно се доказва, че дъгите A'B' и B'C' са с дължини съответно x и y. Освен това, понеже имат обща точка, двете дъги общо формират една по-голяма дъга A'B'C'. Ако точка D попадне вътре в дъгата A'B'C', то центъра на окръжността ще е вътре в един от двата триъгълника DAB или DCB, т.е. центъра ще е вътре и в четириъгълника ABCD. Вероятността за това е:
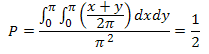
Трябва да отбележим, че това съвпада с вероятността точките да НЕ лежат в една полуокръжност. Действително от миналата задача знаем, че вероятността точките да лежат в една полуокръжност е 1/2, следователно вероятността да НЕ лежат в една полуокръжност е (1-1/2) = 1/2.
Задача 5. "n" на брой точки лежат върху една окръжност. Каква е вероятността центърът на окръжността да лежи вътре в n-ъгълника, образуван при свързването на всеки две съседни точки с отсечка?
Недоказано решение: Хипотезата е, че вероятността е обратната на вероятността всички точки да лежат в една полуокръжност, т.е. решението на тази задача ще е P=1-2n/2n. Проверете дали е така или не е!
Задача 2 :
Това е вероятността четирите точки да лежат в избраната от нас полуокръжност. Вероятността четирите точки да лежат в някоя произволна ПО трябва да е 1/8 :
Вероятността първата т-ка лежи в/у коя да е ПО от кръга е 100% = 1. Вероятността за вс. следваща е 1/2. Умножаваме ги , понеже са независими и получаваме 1/8.
Ако сме фиксирали полуокръжностите ( тоест ние сме си ги избрали ) , не трябва ли да сметнем и вероятността точките да не са в никоя полуокръжност ( да лежат на правата м/у 2-те ПО ) ?
няма - избираш фиксирана полуокръжност и гледаш дали другите три точки ще попаднат в нея, а това е погрешно. В задачата се иска друго.
Вероятността две произволни точки да са краища на един диагонал (т.е. да не може да се каже в коя полуокръжност са) е точно 0. Геометричната вероятност е "дължината, което вземат точките / дължината на окръжността". Точките са едномерни, т.е. дължините им в двумерното пространство са нула, а от там и вероятността е нула. В други задачи от раздел "Вероятности" съм описал това.