C, PHP, VB, .NET

Забележка: В тази статия съм изказал хипотеза, които не съм доказал строго. Възможно е решенията на задачите и изводите от тях да не са вярни, защото те стъпват на тази хипотеза! Надявам се да не се изложа, но още повече се надявам да не подведа никой. Приемете тази статия като „несигурна чернова“.

От предишната статия в Задача 3 използвахме, че една точка в окръжност и центъра на окръжността определят две полуокръжности, две точки и центъра определят четири полуокръжности, …, n точки и центъра определят 2n полуокръжности. Това е естествено, защото всяка избрана лежаща на окръжността точка и центъра на окръжноста определят права, която разделя окръжността на две равни части. Как стои положението в тримерното пространство при сфера?

Очевидно е, че една точка лежаща върху повърхнината на сферата и центъра не са достатъчни, за да се определи полусфера. Представете си например Земята и точката на северния полюс – през нея може да минават безброй много паралели, всеки един от които определя полусфера. При две точки нележащи на един диагонал обаче полусфера може да се определи еднозначно. Това също е логично, защото тези две точки заедно с центъра на окръжността определят еднозначно една равнина, която разделя сферата на две полусфери. Ето пример:

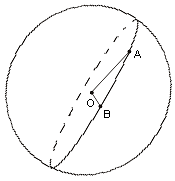Колко полуокръжности определят три точки? Това са комбинациите между трите точки, умножени по две (всяка комбинация определя две полуокръжности). От тук можем да намерим формула и за „n“ точки. Всеки n≥2 точки, нито две от които нележащи на един диагонал, определят общ брой полусфери по формулата:

Сега по индукция бих искал да изкажа следното твърдение:

Твърдение: За всяка „k“ мерна хиперсфера, всеки „n“ точки (n≥k-1), нито две от които нележащи на един диагонал, определят следният брой „полухиперсфери“ с центъра:

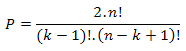Доказателството на това твърдение оставям за по-добри математици от мен. Аз тук ще направя само…

Проверка: при окръжност имаме k=2. Следователно:

n=1 => 2.1!/1!.0! = 2 полуокръжности
n=2 => 2.2!/1!.0! = 4 полуокръжности
n=3 => 3!/1! = 6 полуокръжности
n=4 => 4.2 = 8 полуокръжности

При сфера имаме k=3. Следователно:

n=2 => 2.2!/2!.0! = 2 полусфери
n=3 => 2.3!/2!.1! = 2.3 = 6 полусфери
n=4 => 2.4!/2!.2! = 12 полусфери
n=5 => 2.5!/2!.3! = 20 полусфери

Нека сега решим няколко задачи.

Задача 1. Дадена е сфера с радиус 1. Каква е вероятността четири произволни точки да лежат в една и съща полусфера?

Решение: Взимаме една произволна полусфера. Вероятността една произволна точка да попадне в нея е 1/2. Следователно вероятността за четири произволни точки ще бъде (1/2).(1/2).(1/2).(1/2) = 1/16.

Тези четири точки определят общо 12 полусфери. Следователно вероятността e:

P=12/16=3/4

Задача 2. Дадена е сфера с радиус 1. Каква е вероятността пет произволни точки да лежат в една и съща полусфера?

Решение: Вероятността за това пет произволни точки да попаднат в една определена полусфера е 1/32. Пет точки определят 20 полусфери. Следователно вероятността e:

P=20/32=5/8

Задача 3. Дадена е сфера с радиус 1. Каква е вероятността „n“ произволни точки (n≥4) да лежат в една и съща полусфера?

Решение: Вероятността n произволни точки да попаднат в една определена полусфера е 1/2ⁿ. Общият брой полусфери, които определят n на брой точки е n.(n-1). Следователно вероятността е:

P=n.(n-1)/2ⁿ

Задача 4. Дадена е „k“-мерна хиперсфера (k≥2) и произволни „n“ на брой точки лежащи върху нея, като n≥k-1. Каква е вероятността всичките n на брой точки да лежат в една „полухиперсфера“?

Решение: Взимаме фиксирана „полухиперсфера“ – вероятността точките да лежат в нея е 1/2ⁿ. Общият брой „полухиперсфери“ според изказаното по-горе твърдение е 2.n!/(k!.(n-k)!). Следователно вероятността е:

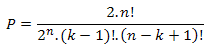Задача за упражнение: Начертайте дискретните графики* на функциите:

f_k=2(n)=2.n/2ⁿ, n≥1

f_k=3(x)=n.(n-1)/2ⁿ, n≥2

f_k=4(n)=2.n.(n-1).(n-2)/(6.2ⁿ), n≥3

f_k=5(n)=2.n.(n-1).(n-2).(n-3)/(24.2ⁿ), n≥4

f_k=6(n)=2.n.(n-1).(n-2).(n-3)/(120.2ⁿ), n≥5

По абцисата ще стоят броят точки (n са цели числа*), а по ординатата естествено ще имате вероятността от 0 до 1 те да се намират в една полухиперсфера. Забелязвате ли някаква зависимост?

* Може и да начертаете графиките на функциите с n реално число, но после я засечете с вертикални линии на всяко цяло n, за да намерите търсените пресечни точки. В тези задачи няма смисъл от изказвания като например „2,3 точки лежащи върху хиперсфера“, защото не е ясно какво означава „0,3 точки“.