* Задачата на Бертран
Публикувано на 23 март 2010 в раздел Вероятности.
Задача: Дадена е окръжност с радиус r и вписан в нея равностранен триъгълник ABC. Каква е вероятността произволна хорда от окръжността PQ да има по-голяма дължина от страната на триъгълник ABC?
Решение 1: Без да ограничаваме решенията „завъртаме“ триъгълник ABC така, че т.A да лежи в средата на дъгата PQ. Нека |AR| = 2r e диаметър на окръжността:
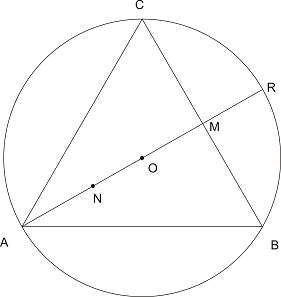
Очевидно PQ ще пресече AR. Нека т.М е пресечната точка на AR с BC. Тогава лесно може да се изчисли,ч е OM=r/2. Построяваме симетричната на т.M точка N спрямо центъра на окръжността. Ако хордата PQ пресече отсечката MN, то дължината |PQ| > |AB|. Знаем, че дължината |MN| = 2r/2 = r. Така вероятността PQ да пресича MN е:
P = |MN| / |AB| = r/2r = 1/2
Решение 2: Без да ограничаваме решенията завъртаме триъгълник ABC така, че точка C да съвпадне с точка P. Така ако т.Q принадлежи на полуравнината определена от ъгъл ACB, то дължината на хордата PQ ще е по-дълга от страната на триъгълника.
Точка Q може да се „движи“ само по окръжността, т.е. в полуравнината определена от допирателната към окръжността в т.С. Така можем да пресметнем вероятността спрямо изправения ъгъл на допирателната, т.е. равен на π. Знаем, че ъгъл ACB = π/3.
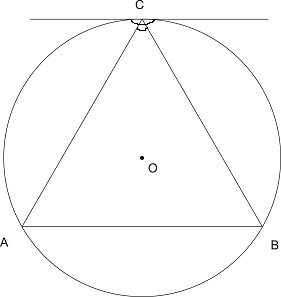
=> P = (π/3)/π = 1/3
Решение 3: Построяваме кръг с център т.O и радиус r/2 (в случая това дори се оказва вписаният кръг в триъгълника):
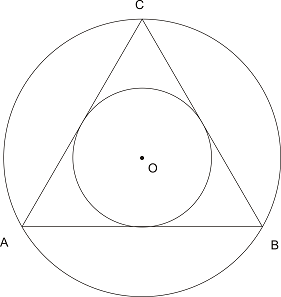
Ако центърът на хордата PQ лежи вътре в този кръг, то тя ще бъде с по-голяма дължина от AB. Вероятността за това е:
P = S(вписаният кръг)/S(описания кръг) = π.(r/2)2/π.(r)2
=> P = 1/4
Обобщение: Колкото и да звучи странно – и трите решения са вярни въпреки, че отговорите са различни! Разликата се получава поради различната гъстота на решенията. Ако проведете поредица от експерименти по показаните методи при произволни хорди ще видите, че всъщност и трите вероятности се удовлетворяват статистически точно. Въпросната гъстота на решенията се променя именно поради „завъртането“ на триъгълника. Но отново казвам – това не прави отговорите грешни. Затова въпросът в условието на задачата трябва да е не „Каква е вероятността…“, а „Каква е вероятността по метода за решение…“. С други думи парадоксът на задачата на Бертран се корени в недоизказано условие. Такива парадокси има налични и в други задачи по вероятности и статистика.
Така дадено условието (за хорда) според мен решението трябва да е 1/3 като отношение на всички възможни хорди към тези които ни удовлетворяват. Решение 3 е за вероятност точка от хордата да е вътре в малката окръжност, но по-дългите хорди имат повече точки в нея от по-късите, от там и грешно решение. За решение 1 още мисля каде е некоректно.
За решение 1 PQ може да е по-дълга от AB и без да пресича MN например успоредна на AB и пресича AN.
mertol – за решение 3 говорим не за „точка от хордата“, а за „център на хордата“. Има сериозна разлика.
За задача 1 мисля, че си прав. Ще проверя решението и ще открия къде съм сгрешил при дефинирането му. Все пак да си призная, че решенията не са мои, а съм ги взел от мои записки по лекции :)
Така, намерих грешката в задача 1 и ще я поправя в условието. Не просто „завъртаме триъгълник ABC така, че т.A да лежи вътре в дъгата PQ„, а „завъртаме триъгълник ABC така, че т.A да лежи в средата на дъгата PQ„. Тоест PQ винаги е перпендикулярна на AR! От там нататък решението си е вярно :)
От решение 3.“Ако центърът на хордата PQ принадлежи на тази окръжност, то тя ще бъде с по-голяма дължина от AB. “ тази хорда ще бъде равна по дължина на страната на триъгълника!
Да, прав си – ще поправя текста. Не „принадлежи на тази окръжност“, а „вътре в кръга“…