* Статистически тест на Ман-Уитни в Excel
Публикувано на 12 септември 2013 в раздел Математика.
В последните дни ми се наложи да си припомням математическата статистика във връзка с дисертацията. Благодарение на доц. Дурева си спестих много време и "грешни сметки", защото тя ме насочи директно към правилния метод за проверка на хипотези спрямо данните, които изследвам. Става въпрос за методът Ман-Уитни (Mann-Whitney U-test). Това е непараметричен метод, с който се сравняват две извадки (може да са с различен обем) и се проверява хипотезата, че са със статистически еднакви медиани. Алтернативната хипотеза естествено е, че едната извадка има статистически значима разлика в медианата спрямо другата.
За мое дълбоко разочарование установих, че този тест не е наличен като готова функция (или data analysis) в Excel. Естествено го има в SPSS и други по-сериозни статистически софтуерни продукти, които аз хем нямам (това не е чак такъв проблем), хем не ми се отделя време да разучавам (а това вече е сериозен аргумент). Намерих сайтове, които или бяха предвидени за извадки до не повече от 20 елемента, или ми бяха неудобни. Намерих и заготовки за Excel, но все защитени (да не може да се копират формулите) - защо им е на авторите това, не ми е ясно. Затова се потрудих малко и си направих следния шаблон:
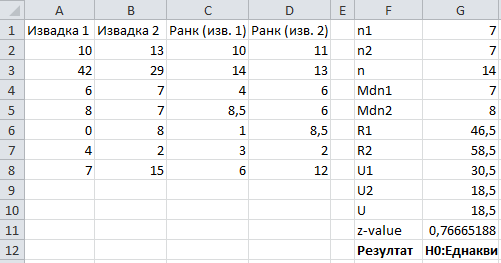
Използвайки тази заготовка трябва просто да сложите данните за първата извадка в първата колонка и данните за втората извадка във втората колона. Евентуално може да се наложи да разтеглите (или изтриете) съответните им стойности в двете колони с ранкингите. Останалото се изчислява в колоната отдясно. При n1 и n2 по-малки от 20 може да използвате таблица за критичните стойности (sheet 2). Иначе може да се доверите на апроксимацията със z-стойността ("резултат", който се изписва в последния ред) - това е по-неточно. Най-голямата таблица на критични стойности, която успях да открия, беше с размерност 34x39. Не успях обаче лесно да я конвертирам към excel и затова оставих стандартната 20x20.
Изтегли заготовката: Mann-Whitney U-тест заготовка
Надявам се да съм бил полезен на поне един човек (освен на себе си).
Впечатляващо, но възникват малко въпроси по описанието:
1. "Това е непараметричен метод, с който се сравняват две извадки (може да са с различен обем)" ... към това бих добавил но не с нормално разпределение и не "чифтни" измервания ... иначе е допустимо да ползваш Т-тест на Стюдънт, а той е с "по-силен" резултат или пък Уйлкоксън (Wilcoxon), който е за липсващо нормално, но за зависими извадки.
3. А защо не използва Колмогоров-Смирнов тест за две извадки (название по SPSS - Two Independent Samples Test), т. е. защо U а не K test. Може да бъркам, но не се сещам да има пречка за прилагането му (пролага се както при една така и при две извадки)
4. Метода който си използвал е: Това е непараметричен, рангов тест, с който се сравняват две НЕПРЕКЪСНАТИ ПРОМЕНЛИВИ, разположени на ОРДИНАЛНА скала в две НЕЗАВИСИМИ извадки (може да са с различен обем), при които се проверява хипотезата, за разлика в разпределенията (вкл. и еднаквост на медианите, на теория би трябвало да проверява дали 50% от случаите попадат под и над общата медиана);
5. Извинявам се ако съм досаден и ако БЪРКАМ някъде, МОЛЯ да ми кажеш
6. ГОЛЯМО МЕРСИ ЗА ЗАГОТОВКАТА. Ако някога ти се наложи, с радост ще ти помогна за начин на работа в SPSS, стига да мога :)
За точната дефиниция, която ти казваш - не мога да направя нищо друго освен да замълча :)
Сравнявам две групи от студенти и оценките, които са получили. В случая проверявам дали в експерименталната група се е повишил успеха на цялата група или не се е.
Като данни получавам, че средното аритметично на експерименталната група е доста по-голямо, но с теста на Ман-Уитни излиза, че медианите са статистически равни. От там (подчертавам - аз) си вадя извода, че само част от експерименталната група (по-изявените студенти от нея) са се повлияли от експерименталното обучение. Огромната дисперсия в експерименталната група също би трябвало да е свидетел за това.
Не съм никак добре по математическа статистика за съжаление. В частност за споменатия от теб тест на Колмогоров-Смирнов не знам нищо в детайли. Само знам, че проверява дали са еднакви разпределенията на двете извадки. Не съм сигурен, че това ще ми помогне (или не знам как).
1. Ясно в експерименталната имаш ляво изтеглена асиметрия/рамо, с ясно видима опашка отдясно и вероятно с остър ексцес в лявата част (това все пак зависи от "огромната дисперсия"), :), и си решил да тестваш различията, което пък ме навежда на мисълта, че и популацията/групата ти е асиметрична .... интересно с ляво или дясно изтеглено рамо :) и дали е с остър ексцес (коеф. на Куртозис).
2. Може да не си добре, но си прав К-S няма никакво отношение, а моя въпрос е ... глупав :)
3. Явно си доста старателен, ако добре си направил извадката е жалко, че контролната ти е увиснала, т. е. Н=0. Hедостоверността е голям проблем, ако цялото ти изследване е около ефекта (корелация или детерминация от прилагани методи). :(
4. Не се отказваш щом си си направил привидно логични хипотези за причината за провала ... сега остава да ги провериш :) ... Само си представям реакцията на студентите от екс., ако им пуснеш тест за измерване на мотивацията и психометричните им характеристики..
Недобрият резултат пак е резултат. Стига да е подходено с правилен научен подход - няма проблеми.
полезно е да - дори и след толкова години след дата на публикуване !
Хиляди благодарности, спестихте ми страшни усилия!