* По-голямото от две произволни числа
Публикувано на 15 декември 2010 в раздел Вероятности.
Задача 1: Иван и Петър си намислят произволно цяло число от 1 до 10. Каква е вероятността числото на Петър да е строго по-голямо от числото на Иван?
Решение: Построяваме координатна система с начало точка (1,1), в която по оста x (хоризонталата) ще нанасяме избраното число от Иван, а по оста y (вертикалата) избраното число от Петър. Получава се квадрат от възможни точки:
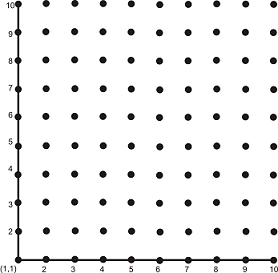
Ако изберат едно и също число, то се намират в една от точките по диагонала:
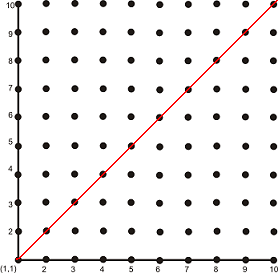
Ако изберем точка от "горно-лявата" половина на квадрата, то числата по вертикала ще са по-големи от числата по хоризонтала, а ако изберем от "долно-лявата" половина обратно. Следователно точките намиращи се в оцветената в зелено част (без задрасканите с червената линия по диагонала - в условието пише "строго по-голямо") ще са тези, при които Петър печели:
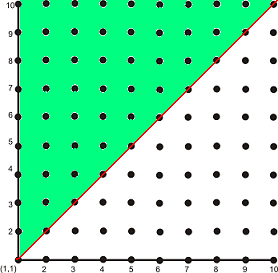
Следователно вероятността Петър да е избрал строго по-голямо число от Иван е:
P = 45/100 = 0,45
Задача 2. Иван и Петър си намислят произволно цяло число от 1 до 10. Каква е вероятността числото на Петър да е по-голямо или равно от числото на Иван?
Решение: Моделът е същият както от миналата задача, но вече трябва да включим и точките по диагонала. Следователно решението е:
P = 55/100 = 0,55
Задача 3. Иван и Петър си намислят произволно цяло число от 1 до 100.
a) Каква е вероятността числото на Петър да е строго по-голямо от числото на Иван?
б) Каква е вероятността числото на Петър да е по-голямо или равно от числото на Иван?
Решение: Очевидно и тук моделът ще е същия, но броят точки ще е различен. Общият брой точки в квадрата е S=10000, а точките по диагонала са d=100. Следователно точките в зелената част (без тези по диагонала) NW=(10000-100)/2=4950. Така получаваме решенията:
P(a) = 4950/10000 = 0,495
P(b) = (4950+100)/10000 = 0,505
Обобщена задача (при ограничено множество). Иван и Петър си намислят произволно цяло число от 1 до n.
a) Каква е вероятността числото на Петър да е строго по-голямо от числото на Иван?
б) Каква е вероятността числото на Петър да е по-голямо или равно от числото на Иван?
Решение: Общият брой точки в квадрата е S=n2. Точките по диагонала са d=n. Точките в зелената част без тези по диагонала са NW=(n2-n)/2. Следователно решенията са:
P(a) = (n2-n)/2n2 = (n-1)/2n
P(b) = (n2+n)/2n2 = (n+1)/2n
Обобщена задача (при неограничено множество). Иван и Петър си намислят произволно цяло число, по-голямо или равно на 1.
a) Каква е вероятността числото на Петър да е строго по-голямо от числото на Иван?
б) Каква е вероятността числото на Петър да е по-голямо или равно от числото на Иван?
Решение: Ще намерим решението на тази задача от решението на предишната при "n" клонящо към безкрайност. Вижда се веднага, че и при двата случая вероятностите са равни:
P(a) = P(b) = 1/2
Задача за упражнение 1: Решете задачи 1 и 2 като този път избраното число може да включва и цифра след десетичната запетая, например 8,6 или 2,3.
Задача за упражнение 2: Решете задачи 1 и 2 като избраното число може да съдържа до "n" цифри след десетичната запетая.
Задача за упражнение 3: Решете задачи 1 и 2 като избраното число може да е реално (т.е. неограничен брой цифри след десетичната запетая).
Задача-уловка: Решете задачи 1 и 2 като избраното число може да е рационално, но НЕ и ирационално.
Тотално обобщена задача: Иван и Петър си намислят произволно реално число (може и отрицателно). Каква е вероятността Петър да е избрал по-голямо число от Иван?
упр. 2 аналогично на упр. 1 умножаваме по 10^n=, избират се числа от 1 до 10*10^n=10^(n+1). Общия брой е 10^(2n+2). Числата под и над диагонала са по (10^(2n+2)-10^(n+1))/2. Вероятностите са:
(10^(2n+2)±10^(n+1))/(2*10^(2n+2))=(10^(n+1)±1)/(2*10^(n+1))
упр.3 Решение
Задача уловка: Ако си изберат числа с равен брой цифри след дес. запетая, задачата се свежда до зад. за упр. 2, като n зависи от това с колко цифри след запетаята са числата на Иван и Петър. Ако числата им са с различен брой цифри, задачата се свежда до упр.3 т.е. 1/2. Това в кой случай попадат също се свежда до упр.3, като шанса да изберат числа с еднакъв брой цифри ->0, така че общото решение на задачата също е 1/2.
упр. 1: за по-лесно умножавам по 10 и се получава същата задача, но си избират числа между 1 и 100. Общия брой им е 10000, числата по диагонала са 100, числата под и над са по 4950. Или вероятностите за зад. 1 и 2 са 49.5% и 50.5%
Поправка - Ако числата им са с различен брой цифри, цифрите в повече на по-дългото може да се игнорират и се свежда до зад. от упр.2 с по-малкото от 2те n. Това в кой случай попадат се свежда до упр.3, като шанса да изберат числа с еднакъв брой цифри ->0, така че общото решение на задачата e усредненото от 2та варианта на упр.2 т.е. 1/2.
За упр1. Точно така - задачата е еквивалентна на задача 3
За упр2. Еквивалентно на "обобщена задача (при ограничено множество)"
За упр3. Еквивалентно на "обобщена задача (при неограничено множество)"
За "задача уловка": рационалните числа тъй или иначе са безкрайно много, т.е. вероятността да са равни е нулева, следователно търсената вероятност е точно 1/2.
Тотално обобщена задача: Очевидно пак 1/2