C, PHP, VB, .NET

В задачата за счупената на три парчета пръчка можехме да „чупим“ пръчката на произволно място. А какво ще се получи ако можем да чупим пръчката на предварително зададени точки, от които можем да си избираме произволно? Ето как ще формулираме такава задача:

Задача 1. Избираме четири точки върху пръчка така, че я разделят на пет равни части. Избираме две произволни точки от тях и чупим пръчката в тях. Каква е вероятноста получените три парчета да могат да са страни на триъгълник?

Решение: Тук решението може лесно да се получи с просто изброяване на всички възможни варианти. Ние ще направим именно това, но ще разледаме едно специфично геометрично решение на задачата. Нека разгледаме координатна система с дискретно разделение. По първата ос ще нанасяме дължината на едно от парчетата, а на другата дължината на второто. Ясно е, че всяко едно парче може да е с дължина 1, 2 или 3. Следователно възможните комбинации от две парчета са:

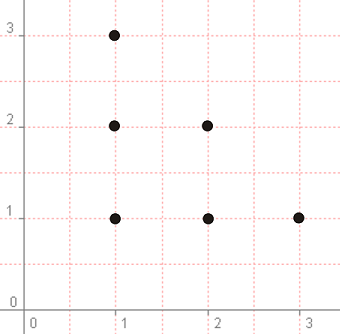
Ако изберем точка (1,1), то няма да имаме триъгълник, защото дължината на третото парче ще е 5-(1+1) = 3, а числата 1,1 и 3 не изпълняват условията за съществуване на триъгълник (3>1+1). Същото важи за точките (1,3) и (3,1). Ще имаме триъгълник само в точки (1,2), (2,1) и (2,2). Виждаме нещо познато – крайните точки формират един голям триъгълник, а решенията вписан чрез медицентровете му:

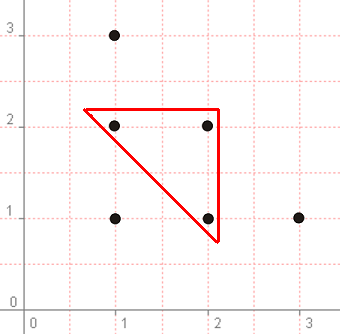
Решението се получава като разделим сбора от точките в червения триъгълник на сбора от всички точки:

P(5 части) = 3/6 = 1/2

Задача 2. Избираме пет точки върху пръчка така, че я разделят на шест равни части. Избираме две произволни точки от тях и чупим пръчката в тях. Каква е вероятноста получените три парчета да могат да са страни на триъгълник?

Решение: Ще направим същия модел. Максималната дължина на парче е 4 единици:

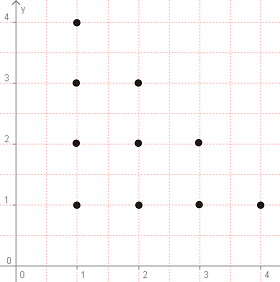
В този случай виждаме, че точките (1,1), (1,2), (1,3), (1,4), (2,1), (3,1), (4,1), (3,2), (2,3) НЕ са решение. Единственото решение е точка (2,2). На пръв поглед изглежда, че този случай няма нищо общо с предишната задача. Всъщност принципът с вписания триъгълник е валиден и тук:

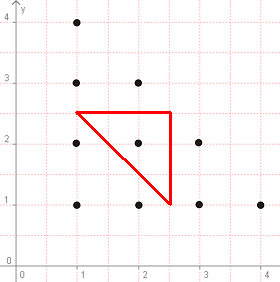
Решението е:

P(6) = 1/10

Задача 3. Намерете P(7).

Решение: Отново правим същия модел. Максималната дължина на парче е 5:

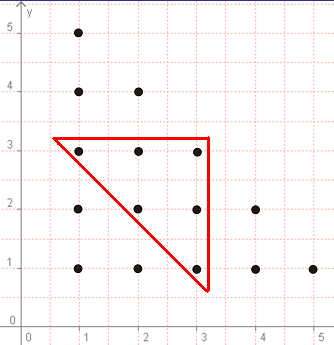
Можете лесно да проверите, че представеното решение е вярно:

P(7) = 6/15 = 2/5

Задача 4. Намерете P(8).

Решение: И тук решението идва по същия метод:

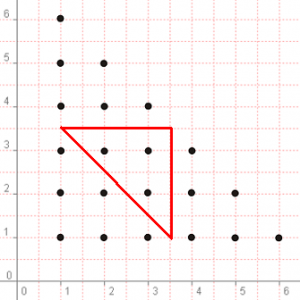
Значи решението е:

P(8) = 3/21 = 1/7

Задача 5 – обобщена: Намерете P(n) за всяко n.

Решение: Тук няма да даваме доказателството подробно (оставяме това за ваша задача). От горните примери се вижда, че има сериозна разлика между случаите, в които n е четно или нечетно. Л. Рейд е изчислил, че при четно n вероятността е:

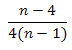
а при нечетно вероятността е:

Докажете, че това е така (нужно е да намерите формули за броя точки в червения квадрат, както и за общия брой точки в триъгълника при четен и при нечетен брой точки).

Изследване: За да направим истинска връзка с предишната задача, то е добре да изследваме границата на двете числови редици при „n“ клонящо към безкрайност. Решението се намира бързо и просто – 1/4 и при четен и при нечетен брой точки! Това напълно съвпада със случаи 1) и 4) от обобщената задача с непрекъснато множество от „точки за чупене“.

Начертайте първите 15 точки в координатна система с оси „n“ (броя части) и „P(n)“ (вероятността от 0 до 1). Ако свържете всички точки (i, P(i)) и (i+1, P(i+1)) от графиката ще видите, че отсечките винаги пресичат правата успоредна на оста „n“ на отстояние 1/4 и освен всичко друго тези отсечки стават все по-къси и по-къси, т.е. все повече и повече се доближаваме до обобщената задача.