C, PHP, VB, .NET

Преди да започнем нека припомним две добре известни задачи и техните решения:

Задача за 9-те точки: Имаме квадратна матрица от 3x3 точки. Свържете всички точки с четири отсечки без да си вдигате ръката от листа.

Решение:

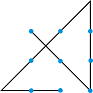
Задача за 16-те точки: Имаме квадратна матрица от 4x4 точки. Свържете всички точки с шест прави отсечки без да си вдигате ръката от листа.

Решение:

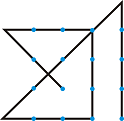
Задача за n-те точки: Имаме квадратна матрица от nxn точки, n>2. Свържете всички точки с 2.n-2 отсечки без да си вдигате ръката от листа.

Решение: Ще изведем алгоритъм на базата на предишните две задачи.

1 случай - нека n е нечетно число) Започваме от главния диагонал - от точка (0,0) до точка (n,n). След това прекарваме отсечка вертикално нагоре и "излизаме с една точка нагоре", т.е. до координати (n, -1). От там под ъгъл 45 градуса по диагонал до точка (-1, n). От там до точка (n-1, n). Продължаваме по спирала от отсечки под прав ъгъл до изчерпване на всички точки.

Пример с матрица 5x5: Очакваме 2*5-2 = 8 отсечки:

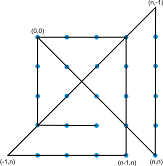
Пример с матрица 7x7: Очакваме 2*7-2 = 12 отсечки:

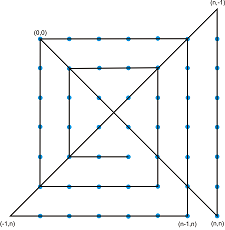
Пример с матрица 9x9: Очакваме 2*9-2 = 16 отсечки:

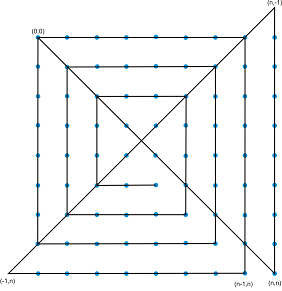
Индукционна хипотеза: Алгоритъмът за построение работи за всяко нечетно n.

Доказателство: Приемаме, че алгоритъмът работи за нечетното число k. Трябва да докажем, че работи за k+2. Матрицата с k+2 точки се получава като добавим два реда и два стълба към матрицата от k точки. Нека ги сложим по такъв начин, че имаме по един ред от горе и от долу и един ред от ляво и от дясно (тоест горния ляв ъгъл на новата матрица ще е (-1,-1), а долния десен (n+1,n+1)).

Сега нека направим същото построение както за матрицата k, но в обратен ред, т.е. започваме от центъра по спиралата и стигаме до точката (0,0). Тук обаче няма да спираме в точка (0,0), а ще продължим последната отсечка до точка (-1,-1). Това продължение не е нова отсечка, тоест дотук имаме 2k-2 отсечки. От точка (-1,-1) прекарваме хоризонтална отсечка до (-1, n+1), с което преминаваме през всички нови точки от горния ред - това е една нова отсечка. От там прекарваме отсечка вертикално надолу до (n+1,n+1) с което преминаваме през всички отсечки от десния стълб на новата матрица - това е втора отсечка. От там отново хоризонтална отсечка до точка (n+1,-1) с което преминаваме през всички отсечки по долния ред на новата матрица - трета отсечка и накрая вертикално нагоре до точка (-1,0) с което преминаваме през всички точки по левия стълб на новата матрица - четвърта отсечка. Значи имаме общо 4 нови отсечки

=> Общия брой отсечки с които сме преминали през всички точки на матрица (k+2)x(k+2) е:

2*k-2+4 = 2*k+4-2 = 2*(k+2)-2

=> индукционната хипотеза е доказана за нечетно n.

Пример от доказателството на индукционната хипотеза от матрица 9x9 до матрица 11x11:

Стъпка 1: Отсечките са 2*9-2 = 16.

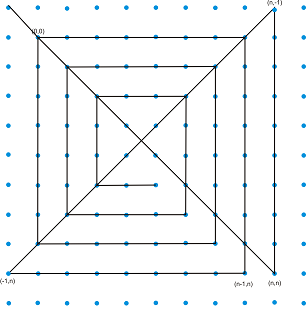
Стъпка 2: Отсечка минаваща през горния ред - отсечките са 17:

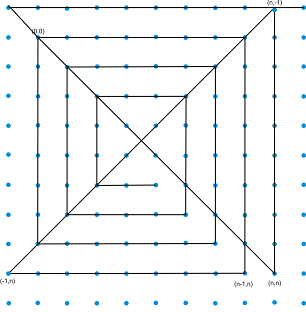
Стъпка 3: Отсечка минаваща по десния стълб - отсечките са 18:

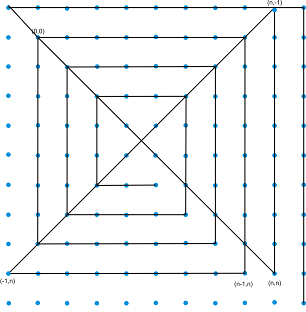
Стъпка 4: Отсечка по долния ред - отсечките стават 19:

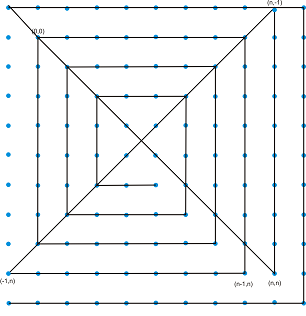
Стъпка 5: Отсечка по левия стълб - линиите са 20 - точно 11*2-2:

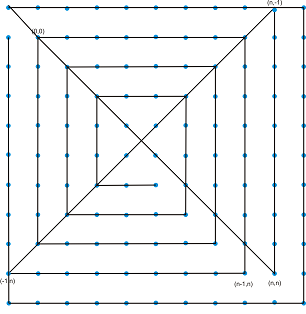
Очевидно е, че от така полученото решение на матрица (k+2)x(k+2) може да се продължи последната отсечка с две точки нагоре (с което отсечките не се увеличават) и от там да се направи нова обиколка от четири отсечки, с което да се покрие матрица от (k+4)x(k+4) с 2*(k+2)-2+4 = 2*(k+4)-2 отсечки. Абсолютно аналогично спиралата може да се продължава до безкрайност => индукционната хипотеза е доказана и за всяко нечетно n>2 можем да свържем матрица с nxn точки с 2*n-2 линии.

2 случай - нека n е четно число) Започваме от точка (n/2+1, n/2). Преминаваме с втора отсечка по диагонал от -45 градуса през 2 точки (ще се намираме в точка (n/2-1, n/2-2)). От там по хоризонтала надясно през три точки до точка (n/2-1, n/2+1). От там по спирала до достигането на точка (n-1, n). От там по хоризонтала до точка (-1, n), после по диагонал до точка (-1, n) и по вертикала до точка (n,n).

Пример с матрица 6x6: Очакваме 2*6-2 = 10 отсечки:

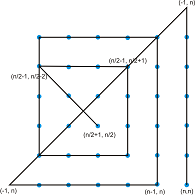
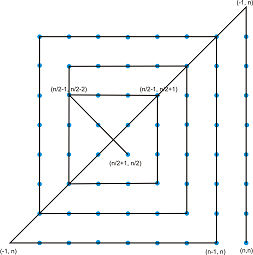
Пример с матрица 8x8: Очакваме 2*8-2 = 14 отсечки:

Индукционна хипотеза: Алгоритъмът за построение работи за всяко четно n.

Доказателство: Приемаме, че алгоритъмът работи за четното число k. Трябва да докажем, че работи за k+2. Отново както в случая на нечетна матрица добавяме по един стълб от ляво и от дясно и по един ред от горе и от долу на съществуващата матрица. Последната отсечка я продължаваме до (n, n+1), с което не увеличаваме текущия брой отсечки (14). От там с четири отсечки "обикаляме" и пресичаме новите два реда и два стълба, с което преминаваме през всички нови точки. Така получаваме общо 2*k-2+4 = 2*(k+2)-2 точки - точно очаквания резултат.

Пример от доказателството на индукционната хипотеза от матрица 8x8 до матрица 10x10:

Стъпка 1: Отсечките са 2*8-2 = 14.

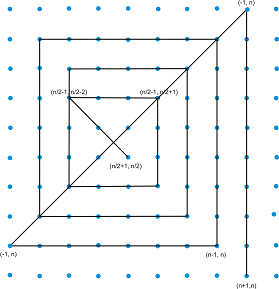
Стъпки 2, 3, 4 и 5: Отсечките са 2*10-2 = 18.

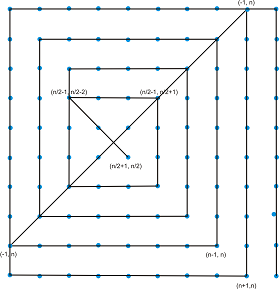
Очевидно е, че от така полученото решение на матрица (k+2)x(k+2) може да се продължи последната отсечка с една точка наголу (с което отсечките не се увеличават) и от там да се направи нова обиколка от четири отсечки, с което да се покрие матрица от (k+4)x(k+4) с 2*(k+2)-2+4 = 2*(k+4)-2 отсечки. Абсолютно аналогично спиралата може да се продължава до безкрайност => индукционната хипотеза е доказана и за всяко четно n>2 можем да свържем матрица с nxn точки с 2*n-2 линии.

Обобщение: Всяка матрица от nxn, n>2 точки може да бъде покрита с 2*n-2 отсечки.

Задача за търсене на минимум: Намерете минималният брой отсечки, които покриват матрица nxn точки.

Решение: В процес на търсене. Хипотезата е, че минималният брой отсечки е 2*n-2.

Тази страница ще бъде обновявана когато се намери продължение в решението на задачата за минимум. Ще се търси компютърен модел за доказване на хипотезата в частни случаи. Всяка помощ от вас е добре дошла...