* Реални корени на квадратно уравнение с a=1
Публикувано на 14 ноември 2012 в раздел Вероятности.
Задача 1. Дадено е квадратното уравнение x2 + bx + c = 0. Каква е вероятността корените му да са реални числа, ако b и c са в интервала [0,1]?
Решение: Корените ще бъдат реални числа тогава, когато дискриминантата на уравнението е положително число. Тя е D=b2-4c.
=> Търсим кога c < b2/4
Ако съставим ортонормирана координатна система в която по остта x нанасяме възможните числа b, а по остта y числата c, то те бидейки в интервала [0,1] определят област на един квадрат. Ако нанесем графиката на функцията y=x2/4, то тя ще отсече следната част от квадрата:
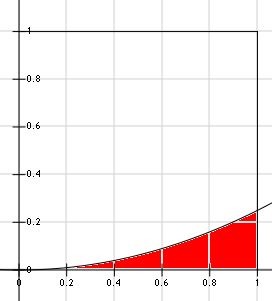Интересуваме се от отношението на площта под функцията и цялата площ на квадрата. Тоест имаме:
[math]P=\frac{\int_{0}^{1}\frac{x^2}{4}dx}{1.1}=\frac{1}{12}[/math]
Задача 2. Какво ще се получи ако b и c са в интервала [0,10]?
Решение: Задачата ще бъде същата, но вече ще имаме по-сложна област:
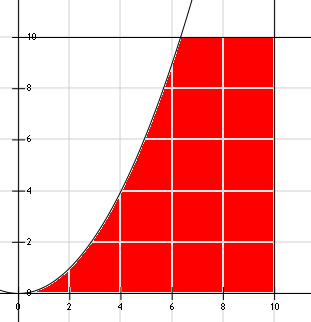Трябва ни пресечната точка на функцията y=x2/4 с функцията y=10.
Заместваме и получаваме [mathi]x^2=40[/mathi] => [mathi]x=\sqrt{40}[/mathi].
=> пресечната точка е с координати [mathi](\sqrt{40}, 10)[/mathi].
Така червената област ще бъде с лице:
[math]S(red)=\int_{0}^{\sqrt{40}}\frac{x^2}{4}dx + (10-\sqrt{40}).10=\frac{\sqrt{40}^3}{12}+10(10-\sqrt{40})[/math]
Това е приблизително равно на 57,84
Лицето на квадрата е 100 =>
[math]P=0,5784[/math]
Задача 3. Какво ще се получи ако b и c са в интервала [0,n]
Решение: Първо трябва да преценим кога функцията ще пресече горната страна на квадрата и кога не. Или търсим за коя стойност на „n“ функцията [mathi]y=x^2/4[/mathi] ще мине точно през точката (n,n). Това очевидно е при n=4.
Значи задачата ще бъде разделена на два случая:
1 случай) n<4
=> търсената вероятност се намира както в първа задача и тя ще е
[math]P=\frac{n}{12}[/math]
2 случай) n>4
Отново трябва да търсим пресечната точка, но този път на y=x2/4 с функцията y=n.
Заместваме и получаваме точката [mathi](x,y)=(c,b)=(2\sqrt{n},n)[/mathi].
Търсим лицето на областта:
[math]S(red)=\int_{0}^{2\sqrt{n}}\frac{x^2}{4}dx + (n-2\sqrt{n}).n=n^2-\frac{4.n^{3/2}}{3}[/math]
Знаейки и лицето на квадрата ще намерим търсената вероятност:
[math]P=\frac{n^2-\frac{4.n^{3/2}}{3}}{n^2}=\frac{3\sqrt{n}-4}{3\sqrt{n}}[/math]
Задача 4. Какво ще се получи ако позволим и отрицателни коефициенти, т.е. ако b и c са в интервала [-n,n]?
Решение: Нека погледнем отново дискриминантата: D=b2-4c
Коефициентът „b“ е повдигнат на квадрат. Следователно графиката на функцията е симетрична относно остта Oy => вероятността няма да се промени.
Ако коефициентът „c“ стане отрицателен, дискриминантата става винаги положителна => корените винаги ще са реални. Или казано по друг начин – ако слизаме надолу от абцисната ос, ние ще увеличаваме червената площ на благоприятните (да бъдат корените реални числа) изходи.
Така ако например n=10, графиката ще бъде:
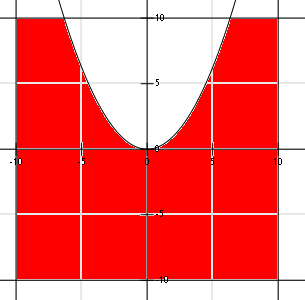
Площта на този червен допълнителен квадрат (в квадрант 4) е n2. Той се добавя и към общата площ, и към площта на благоприятните изходи, т.е. след опростяване ще имаме следното общо решение:
[math]P_{n>4}=1-\frac{2}{3\sqrt{n}}[/math]
[math]P_{n\leq 4}=\frac{n+12}{24}[/math]
Абе математиката ми е малко далечна вече, но тук:
> Ако “a” е различно от нула, ние спокойно можем да разделим двете страни на равенството на него и то няма да се промени. Затова надолу в задачата ще разглеждаме квадратно уравнение от вида x2 + bx + c = 0.
Не трябва ли да се получи уравнението x2 + bx/a + c/a = 0?
Или то се има предвид че b/a пак е някаква форма на b (число) и c/a – форма на c :)
Хмм, последният резултат е доста интересен. Когато n клони към безкрайност, вероятността клони към 1. Това значи ли че в общия случай, при абсолютно произволни b и c вероятността е почти 1? (Не виждам как може да се пресметне точно). Но това е малко отнесен въпрос. Иначе можеш да разгледаш и вариантът когато интервалът е от вида [n, m].
П.п. Всъщност, ако нямаме ограничения (n Е безкрайност), ние всъщност имаме отворен интервал и не можем да сметнем лицето (интеграла). Така че въпросът какво става ако нямаме ограничения е некоректен. Иначе ако разглеждаме интервал, несиметричено отностно 0-та, биха произлезли интересни задачи за търсене на интервал с макс/мин вероятност за реални/имагинерни корени.
Към Иван и Валентин,
Редактирах статията. Все пак си мисля, че с много лека ръка обобщих за [mathi]ax^2+bx+c=0[/mathi]. Ще го мисля още.
Освен интервалите има и още нещо – трябва да се разгледат два случая – a>0 и a<0.
Правилно си обобщил, но с една уговорка. Ти разглеждаш b и c да са в интервала [-n,n]. Но тази уговорка я правиш преди да си разделил на a. В такъв случай просто трябва да разгледаш различен интервал. Например, нека в общия случая b = b_1*a, c = c_1*a. Тогава дискриминантата е a^2(b_1^2 – 4c_1). a^2 > 0 (a е реално), a за другите скоби вече имаш готово решение. Само че ако в началото си тръгнал с b,c в интервала [-n, n], сега трябва да разгледаш b,c в интервала [-n/|a|, n/|а|]. Трябва да вземеш предвид обаче че 4-ката те „прецаква“ и нещата не са чиста монета. Т.е. вероятността ще е различна в случаите n/|a| 4. Или казано с други думи |a| n/4. Съответните вероятности (тук обаче ни трябва ограничение и за а) трябва да се сметнат и от там е лесно. Принципно мисля че с този подход може да се обобщи, но е доста трудно. Може би по-добрият варинт е просто да сметнеш един интеграл от ф-я на две променливи.
Така, и след глупава грешка (скоба на грешно място), тук се получи КОРЕННО различен отговор за n>4. Сега нещата добиха доста по-приличен вид!
Скоро ще пусна и статия с обобщението.
Общото решение: https://www.cphpvb.net/probability/8386-real-roots-of-quadratic-equation/