C, PHP, VB, .NET

Математическата индукция с база различна от 1 се прилага за твърдения P(n), които са вярни за всяко n > k, но не са вярни при n <= k. На практика при тях методът за доказване е абсолютно същия както със старндартната индукция, но вместо да проверяваме базата P(1) ние проверяваме базата P(k+1). Стъпката на доказване на индукционната хипотеза остава същата.

Тези задачи обаче се срещат много по-рядко в училищните програми. Причините са ясни – тъй или иначе задачите с използване на индукция са достатъчно трудни за учениците. Затова индукция с база различна от 1 се показва само на по-талантливите ученици.

Нека разгледаме няколко примерни задачи:

Зад. 1. Да се докаже, че за всяко естествено число n>2 e вярно неравенството 2ⁿ > 2n + 1.

Зад. 2. Да се докаже, че за всяко естествено число n>3 e вярно неравенството 2ⁿ > 2n + 5.

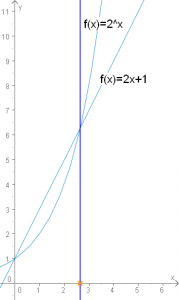
Доказателството на индукционната хипотеза на тези задачи не е толкова тривиално, колкото при показаните в предишната статия за индукция с база 1. Затова обикновено показваме само графично решение на задачата  и не даваме строго такова. Графичното решение се изразява в това да представим изразите от двете страни на неравенството като функции f(x) и g(x) и да покажем, че графиката на f(x) е винаги „отгоре“ над графиката на g(x) след определена стойност x=a (и естествено именно a ще съвпадне с базата на индукцията). Ето например графиката на функциите от задача 1:

Именно в тези задачи (с неравенства) можем да накараме учениците да преоткриват индукционната хипотеза. Например:

Зад. 3. Да намери за кои цели положителни числа n е вярно неравенството 2ⁿ > n²

Тук трябва да направим именно графиките на функциите и чрез тях едновременно да открием базата и да покажем графично решението на индукционната хипотеза.

Има и задачи с рекурентна зависимост на n-тия член към повече от един предходни члена. Така получаваме двойна или по-голяма база на индукцията. Например задачата:

Зад. 4. Дадена е числовата редица a_n = 4.a_n-1 – 3.a_n-2. Ако a₁ = 3, а a₂ = 9 докажете, че за всяко n ⇒ a_n = 3ⁿ.

Решение: Проверка на индукционната база:

a₁ = 3 = 3¹ – вярно
a₂ = 9 = 3² – вярно
⇒базата е вярна.

Доказателство на индукционната хипотеза:

Приемаме, че твърдението е вярно за k-1 и k-2, т.е.

a_k-1 = 3^k-1 и a_k-2 = 3^k-2

Тогава знаем, че:

a_k = 4.a_k-1 – 3.a_k-2 = 4.3^k-1 – 3.3^k-2 = 4.3^k-1 – 3^k-1 = 3^k-1.(4-1) = 3.3^k-1 = 3^k

⇒ индукционната хипотеза е вярна.

Накрая само ще споменем за най-трудните задачи свързани с математическата индукция. Това са задачите, в които трябва да се открие индукционната хипотеза. При тях твърдението, което трябва да се докаже не е дадено в условието на задачата. Това обикновено са много трудни задачи, с които се справят само по-добрите ученици. Ето няколко примера:

Зад. 5. Намерете на колко е равна сумата 1 + 2 + 3 + … + n

Зад. 6. Намерете на колко е равна сумата 1.2 + 2.3 + 3.4 + … + n.(n+1)

Зад. 7. Намерете на колко е равна сумата 1/(1.2)  + 1/(2.3) + 1/(3.4) + … + 1/((n-1).n)

Задачите от примерите са взети от книгата „Методика на обучението по математика (обща част), Благоевград 2002“.