C, PHP, VB, .NET

Нека за удобство приемем, че работим със стандарт RGB24. Вече знаем, че за всеки пиксел се пазят три числа в интервала [0; 255]. Искаме на направим т.нар. "upscale" - да направим изображението по-голямо (с по-голям брой пиксели по хоризонтала и вертикала). Има три популярни алгоритъма за извършване на това и ще разгледаме всеки един от тях поотделно с прости примери.

Алгоритъм "най-близък съсед" (nearest neighbor)

Нека започнем с едно примерно квадратче от 2х2 пиксела:

R: 100 G: 160 B: 140	R: 200 G: 140 B: 160
R: 150 G: 150 B: 150	R: 350 G: 200 B: 100

Искаме да го разтеглим така, че да стане 4х4 пиксела, т.е. да попълним числата в следната таблица:

R: ___ G: ___ B: ___	R: ___ G: ___ B: ___	R: ___ G: ___ B: ___	R: ___ G: ___ B: ___
R: ___ G: ___ B: ___	R: ___ G: ___ B: ___	R: ___ G: ___ B: ___	R: ___ G: ___ B: ___
R: ___ G: ___ B: ___	R: ___ G: ___ B: ___	R: ___ G: ___ B: ___	R: ___ G: ___ B: ___
R: ___ G: ___ B: ___	R: ___ G: ___ B: ___	R: ___ G: ___ B: ___	R: ___ G: ___ B: ___

 

При този алторитъм използваме т.нар. "проксимална интерполация". При него трябва да вземем съществуващите пиксели и да ги повторим. Нека за старт да вземем по-простия линеен вариант на задачата - матрицата от пиксели ще е само с един ред - първия ред в оригиналната таблица:

№0	№1
0%	100%
R: 100 G: 160 B: 140	R: 200 G: 140 B: 160

В заглавните клетки обозначихме, че първият пиксел се намира в началото на реда (0%), а вторият пиксел се намира в неговия край (100%). Новият ред, който трябва да се попълни, ще бъде следният:

№0	№1	№2	№3
0%	25%	50%	100%
R: ___ G: ___ B: ___	R: ___ G: ___ B: ___	R: ___ G: ___ B: ___	R: ___ G: ___ B: ___

Ще разгледаме новата таблица като една линия с начало в 0,0 (0%) и край в 1,0 (100%). Взимаме нулевата клетка №0. Нейното разстояние от началото на линията е 0,0. Умножаваме по най-големия номер от първата таблица - 1 - и получаваме пак 0,0. Закръгляваме и естествено пак се получава 0. Следователно в първата клетка слагаме пиксел №0 от оригиналната таблица:

№0	№1	№2	№3
0%	25%	50%	100%
R: 100 G: 160 B: 140	R: ___ G: ___ B: ___	R: ___ G: ___ B: ___	R: ___ G: ___ B: ___

Взимаме клетка №1. Нейното разстояние от началото на линията е 25%, т.е. 0,25. Умножаваме по най-големия номер от първата таблица - 1 - и получаваме 0,25. Заклъглено това е 0. Следователно във втората клетка слагаме пиксел №0 от оригиналната таблица.

№0	№1	№2	№3
0%	25%	50%	100%
R: 100 G: 160 B: 140	R: 100 G: 160 B: 140	R: ___ G: ___ B: ___	R: ___ G: ___ B: ___

Взимаме клетка №2. Нейното разстояние от началото на линията е 50%, т.е. 0,50. Умножаваме по най-големия номер от първата таблица - 1 - и получаваме 0,50. Заклъглено това е 1. Следователно във третата клетка слагаме пиксел №1 от оригиналната таблица.

№0	№1	№2	№3
0%	25%	50%	100%
R: 100 G: 160 B: 140	R: 100 G: 160 B: 140	R: 200 G: 140 B: 160	R: ___ G: ___ B: ___

Взимаме клетка №2. Нейното разстояние от началото на линията е 100%, т.е. 1,0. Умножаваме по най-големия номер от първата таблица - 1 - и получаваме 1,0. Заклъглено това е 1. Следователно в четвъртата клетка слагаме пиксел №1 от оригиналната таблица.:

№0	№1	№2	№3
0%	25%	50%	100%
R: 100 G: 160 B: 140	R: 100 G: 160 B: 140	R: 200 G: 140 B: 160	R: 200 G: 140 B: 160

Как да постъпим в двумерния вариант на задачата, т.е. когато трябва да разширим цялата матрица, а не само един неин ред? Отново ще приложим проксималната интерполация, но вече с алгоритъм за две размерности. Общата формула за изчисление на произволна клетка в резултатната таблица е:

    X_нова_таблица * най-голям-номер-ред-стара
X = ------------------------------------------
            най-голям-номер-ред-нова
 
    Y_нова_таблица * най-голям-номер-колона-стара
Y = ---------------------------------------------
            най-голям-номер-колона-нова

Тук под Х разбираме номер на ред, а под Y номер на колона. Разбира се работим с цели числа, т.е. трябва резултатите да се закръгляват. Да проверим. Ако вземем например клетка (1,3) от товата таблица, ще имаме следната формула (припомняме, че индексирането започва от нулев елемент!):

X_стара_таблица = закръглено(1 * 1 / 3) = 0
Y_стара_таблица = закръглено(3 * 1 / 3) = 1

Следователно в клетка (1,3) от новата таблица трябва да сложим стойността на клетка (0,1) от старата.

Ето изчисленията от попълването на цялата нова таблица (припомняме, че на места се получава индекс по-голям от максималния в старата таблица и там взимаме последния):

X=0*1/3=0 Y=0*1/3=0 .	X=0*1/3=0 Y=1*1/3=0 .	X=0*1/3=0 Y=2*1/3=1 .	X=0*1/3=0 Y=3*1/3=1 .
X=1*1/3=0 Y=0*1/3=0 .	X=1*1/3=0 Y=1*1/3=0 .	X=1*1/3=0 Y=2*1/3=1 .	X=1*1/3=0 Y=3*1/3=1 .
X=2*1/3=1 Y=0*1/3=0 .	X=2*1/3=1 Y=1*1/3=0 .	X=2*1/3=1 Y=2*1/3=1 .	X=2*1/3=1 Y=3*1/3=1 .
X=3*1/3=1 Y=0*1/3=0 .	X=3*1/3=1 Y=1*1/3=0 .	X=3*1/3=1 Y=2*1/3=1 .	X=3*1/3=1 Y=3*1/3=1 .

Извършвайки сметките и закръгляванията им, получаваме:

R: 100 G: 160 B: 140	R: 100 G: 160 B: 140	R: 200 G: 140 B: 160	R: 200 G: 140 B: 160
R: 100 G: 160 B: 140	R: 100 G: 160 B: 140	R: 200 G: 140 B: 160	R: 200 G: 140 B: 160
R: 150 G: 150 B: 150	R: 150 G: 150 B: 150	R: 350 G: 200 B: 100	R: 350 G: 200 B: 100
R: 150 G: 150 B: 150	R: 150 G: 150 B: 150	R: 350 G: 200 B: 100	R: 350 G: 200 B: 100

Изпробвайте да разширите оригиналната таблица до размери 5х5.

Проксималната интерполация, с която се постига реализирането на алгоритъма за "най-близък съсед", е добра за графики, които трябва да съхранят своята "пикселизация". При този метод няма преливане на цветовете от една точка в друга точка - има просто тяхно копиране. По този начин "назъбените" линии ще си останат назъбени. Например следната малка картинка:

Ще бъде увеличена тройно до тази:

Ако увеличите дори още повече, ще видите, че квадратните пиксели се уголемяват (и си остават квадратни), като не се внася никакъв никакъв шум в бялото пространство между тях или около тях. Ето как ще изглежда още по-силно уголемяване на само малък фрагмент от картинката:

Казано по друг начин, при уголемяване на изображения по метода за "най-близък съсед" се запазва качеството им. Ако след уголемяване те се смалят обратно до оригиналния си размер, обикновено се връщат в точния си първоначален вид - може да има минимални разминавания в рамките на отделни пиксели, като причинител за това ще са закръгленията, когато някой пиксел е точно по средата на линията между други два (0,50 е точно по средата между 0 и 1, но избираме да го закръглим нагоре, т.е. избираме съседа в дясно, а не в ляво).

Колкото до намаляването на изображения - същият метод естествено е приложим и за тази дейност. Трябва обаче да се досетим, че при намаляване на изображението неминуемо ще се изгубят пиксели - ще има такива от старата матрица, които няма да бъдат пренесени в новата. Така може спокойно да се каже, че се губи от качеството. Ето примери за това. Ако вземем следната оригинална картинка (дали снимката е с малко на брой цветове като дадената или не, не е от значение):

Ако я намалим до много малък размер:

И след това я увеличим обратно до оригиналния, ще получим:

Очевидно е, че огромно количество от информацията се е загубила в процеса на downscale. При това, за разлика от това, което показват по филмите, информацията е невъзстановима.

В днешно време скалирането на изображения по метода "най-близък съсед" се използва например при емулирането на стари електронни игри при разтягането им на цял екран (например до 1080p или 4K). Ако играчът желае да получи точен (оригинален) образ от играта, независимо от това, че ще получи остри ръбове и "пикселизирана" картина, това е един адекватен и много бърз алгоритъм за рязтягане на изображенията. По-скоро ще е неподходящ при разтегляне на снимки, защото там бихме очаквали преливания на цветовете и "замазване" на нащърбените от пикселизация линии. За тези цели се използват други алгоритми.

Билинейна трансформация

При този алгоритъм се разчита на създаване на плавни преливания между пикселите. Ако например имаме числата:

1 3

и искаме да вмъкнем трето X между тях, неговата стойност ще е средното аритметично на двата му съседа - (3+1)/2 = 2:

1 2 3

Ако пък искаме между тях да вмъкнем две числа, ще получим:

1 5/3 7/3 3

Защо се получиха точно те? Ако мислено прокараме отсечка от числото 1 до числото 3 и я разделим на четири части за четирите съответни числа, които трябва да напишем, то второто число - 5/3 - ще бъде на разстояние 1/3 от 1 и на 2/3 от 3. Именно 1*2/3 + 3*1/3 = 5/3. Същото е и за третото число: 7/3 = 1*1/3 + 3*2/3.

Тоест в случая ние извършваме плавно преливане от едното число в другото. Какво се случва в двумерния случай? Нека имаме следния квадрат от числа:

1 3
4 2

Ако искаме разширим този квадрат до размери 3х3, ще трябва да намерим общо 5 нови числа, които засега ще запишем с букви:

1 A 3
B C D
4 E 2

Ето как можем да ги намерим:

• A се намира между 1 и 3, т.е. A=2.
• B се намира между 1 и 4, т.е. B = 2,5
• D се намира между 3 и 2, т.е. D = 2.5
• E се намира между 4 и 2, т.е. E = 3
• C се намира или между A и E, или между B и D. Независимо кой от двата случая разгледате, ще получите, че C = 2.5

Ако разтеглим още повече по хоризонтала или вертикала, просто трябва да разграфим линиите между всеки две двойки числа с повече нови точки и при пресмятането да ги умножаваме по съответната пропорция.

При реалните картинки вместо единични числа, както е в примера, ще има вектори от тройки числа - RGB. От там насетне сметките ще бъдат същите, но с една условност - къде точно ще попаднат оригиналните точки, от които започва процеса на интерполация?

Ще вземем един нагледен пример. Взимаме следните четири пиксела:

Разтегляме ги до размер 10х10:

Може би усетихте какво се случи, но все пак ще отбележим с червени кръгчета къде точно са позиционирани оригиналните пиксели, за да се види по-ясно:

Вместо да се разположат в четирите върха на разтеглената картинка (както хората обикновено интуитивно предполагат преди нагледния пример), оригиналните пиксели се разполагат що годе центрирано в нея (на по 1/3 разстояние от всеки ръб, но естествено закръглено към цяло число). Вътре в квадрата, който оригиналните пиксели образуват, се извършват споменатите преливания. В четирите квадрата, които се определят от върха на големия квадрат и най-близкия до него оригинален пиксел, се прави просто повторение на цвета на пиксела (по-големите едноцветни квадрати при върховете). Всички останали пиксели се довършват отново с преливане.

Нека покажем същото нещо, но стъпка по стъпка с преоразмеряване на изображение от 3х3 пиксела на 9х9, направено стъпка по стъпка. Започваме със следната заготовка:

Взимаме празно изображение 9x9, в което нанасяме оригиналните пиксели на новите им позиции:

Сега между всеки два пиксела извършваме "преливане" по начина, по който го направихме по-горе:

Продължаваме по същия начин с белите правоъгълници в средата:

Накрая повтаряме всеки пиксел до ръбовете на изображението:

Софтуерните продукти понякога правят допълнителни оптимизации, с които се опитват да постигнат по-добър преливащ ефект при ръбовете на изображението (и не само). Затова ако си направите тест, ще видите, че при едни и същи входни данни, различните софтуери постигат леки отклонения в цветовете. Например последното преоразмеряване извършено с Paint.Net с филтър приложен като "bilinear" ще даде следния резултат:

Виждате, че прилича на нашето, но има тънки разлики, които са най-видими по ръбовете. Ако вземете точните тройки числа, ще видите, че при преоразмеряването на Paint.Net дори оригиналните пиксели не са точно същите, каквито бяха преди (дори черното и бялото не са абсолютно точни черно и бяло). Няма еднозначно наименование за оптимизациите, които различните софтуерни продукти правят - само понякога се срещат по-специфични наименования като "bilinear-smooth", "bilinear-sharp" и т.н.

Билинейната трансформация не е подходяща за изображения, в които желаем да запазим пикселизацията и назъбените линии. Нека вземем отново изображението с пикселите от по-горе (многото точки), да го увеличим тройно, но с билинейна трансформация, и да се вгледаме отново в малък отрязък:

Вижда се ясно, че около оригиналните точки (пиксели), които бяха на картинката, се получи нещо като "размазване", т.е. изгубихме пикселизацията и острите ръбове, които имаше оригинала.

За сметка на това билинейната трансформация ще даде доста по-добри резултати при снимки. Нека вземем първата снимка на детето и отново да я свием много:

и да я увеличим пак, но с билинейна трасформация:

Виждате, че очевидно се изгуби информация заради свиването, но този път опитът ни за "връщане обратно" показа по-малко пикселизация и се направи опит за по-загладени ръбове. Така, че можете да запомните, че от практична гледна точка билинейната трансформация леко "замазва" картинката и изглажда ръбовете по нея.

Бикубична трансформация

Математиката зад бикубичната трансформация е доста по-сложна спрямо предишните две. Искаме отново да направим преливане на цветовете от една точка към нейна съседна, но този път то да е съобразено и с другите съседи на тези две точки. По този начин целим да направим преходите между тъмни и светли зони по-остри, т.е. да се постигне по-добър контраст по ръбовете на изображението вместо замазването, което беше видно при билинейната трансформация.

Както самото име подсказва, вече няма да интерполираме с линейна функция, а с кубична. Нека започнем с едномерния случай. Ако са дадени две точки A и B, ние търсим функция от вида:

[math]f(x)=ax^3 + bx^2 + cx + d[/math]

която да премине през тези две точки. Производната на f(x) е:

[math]f^{\prime}(x)=3ax^2 + 2bx + c[/math]

Ако приемем, че A е точката x=0, а B е точката x=1, можем да пресметнем веднага, че:

[math]\left|\begin{array}{c}
f(0) = d \\
f(1)=a+b+c+d \\
f^{\prime}(0)=c \\
f^{\prime}(1)=3a+2b+c
\end{array}
\right.[/math]

Ясно е, че от тук може да изразите a, b, c и d - имате четири уравнения с четири неизвестни:

[math]\left|\begin{array}{c}
a = 2f(0) - 2f(1) + f^{\prime}(0) + f^{\prime}(1) \\
b = -3f(0) + 3f(1) - 2f^{\prime}(0) - f^{\prime}(1) \\
c = f^{\prime}(0) \\
d = f(0)
\end{array}
\right.[/math]

Именно това довежда и до формулата за извършване на кубична интерполация между две точки. Имайки тази функция, ние можем да пресметнем стойността на всяка нова точка, която искаме да вмъкнем между дадените две.

Проблемът е с намирането на производната на функцията. Реално ние нямаме самата функция [mathi]f(x)[/mathi], а са ни дадени само няколко нейни точки (не работим с векторни, а с растерни графики, т.е. ние имаме едно изображение съставено от прекъснати точки между които не знаем какво има и съответно няма как да определим каква е функцията, която ги описва). Ние не знаем [mathi] f^{\prime}(A)[/mathi] и [mathi] f^{\prime}(B)[/mathi] и съответно не можем да изчислим коефициентите, които ни трябват, за да направим сметките.

Един вариант е да приемем, че производните са 0. Полученият резултат няма да е много лош. По-добър резултат обаче се получава когато вземем съседните точки на A и B отляво и отдясно, и изчислим "наклона" на графиката на функцията спрямо тези две точки - средното аритметично. По конкретния пример, ако вземем двете съседни на 0 и 1 точки -1 и 2, ще получим следните зависимости за на производните:

[math]\left|\begin{array}{c}
f^{\prime}(0)= \frac{f(1)-f(-1)}{2}\\
f^{\prime}(1)= \frac{f(2)-f(0)}{2}
\end{array}
\right.[/math]

Нека демонстрираме с конкретни стойности какво се случва. Нека [mathi]f(-1) = 4, f(0) = 3, f(1) = 5[/mathi] и [mathi]f(2) = 1[/mathi]. Искаме да интерполираме между точките 0 и 1. Заместваме и получаваме функцията:

[math]\left.\begin{array}{c}
f(x) =(-\frac{1}{2}f(-1)+\frac{3}{2}f(0)-\frac{3}{2}f(1)+\frac{1}{2}f(2))*x^3+\\
+ (f(-1)-\frac{5}{2}f(0)+2f(1)-\frac{1}{2}f(2))*x^2+\\
+ (-\frac{1}{2}f(-1)+(1/2)f(1))*x+\\
+ f(0)
\end{array}
\right.[/math]

В крайна сметка функцията, която интерполира точките с x=0 и x=1 стана:

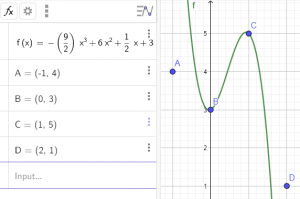
[math]f(x)= -\frac{9}{2}x^3 + 6x^2 + \frac{1}{2}x + 3[/math]

Нека видим нейната графика (кликнете върху картинката, за да уголемите):

 

Виждате, че кривата минава точно през точките B и C. Ако приемем, че B е един пиксел, а C е друг пиксел, то всяка точка между тях, чиято стойност изчисляваме чрез намерената функция, ще бъде стойността на новия пиксел. За разлика от горния пример, функцията f ще връща не единична стойност, а тройка стойности - вектор RGB.

Естествено не сте ограничени в точките 0 и 1. Може да смените съответните числа и ще получите други точки и съответната интерполация между тях. Важното е за всеки две две точки с x=a и x=b, a<b, да има техни съседни отляво и отдясно (x=a-1 и x=b+1).

Какво обаче правим с крайните точки - най-лявата и най-дясната в реда? Тук вече нещата търпят интерпретация. Един вариант е да приемете производните за 0. Друг е просто да повторите стойността на първата точка за нейна лява и съответно на последната точка за нейна дясна. И т.н. В крайна сметка говорим за пиксели, които са извън картинката - такива, които изображението не е регистрирало. Те може да са всякакви, но в общия случай най-добър резултат се получава като се приемат, че са същите както тези по ръба.

Това е едномерния случай - когато имаме един ред с пиксели. Картинките обаче са двумерни. Тук се явява разширението на кубичната интерполация - бикубична. Вече ще ни трябват не 4, а 16 точки. Ако за пример вземем региона [0;1]x[0;1], той е съставен от четири точки (пиксела). Добавяйки нов ред под, над, вляво и вдясно от тях се получава именно матрица от 16 точки (пиксела). Съответно може да се извърши интерполация на двете вътрешни двойки първо по хоризонтала, а после по вертикала. Получената функция с два параметъра ще е интерполираща за региона - чрез нея ще може да се вмъкнат нови пиксели вътре в региона.

Формалният запис на двумерния случай включва употребата на матрични уравнения. Целта на тази статия не е да задълбава в математиката, а да изясни общите принципи, по които се случват нещата. Затова няма да даваме нагледен (при това трудно, защото е триизмерен) пример на интерполацията.

Нека видим какво ще се случи с тестовите ни изображения при билинейна транформация. Първо картинката с пиксели:

Виждате, че се получава размазване около пикселите, което е сходно с това, което се случи при билинейната трансформация. При примера с детето ще се получи доста сходен резултат. За нагледност ще дадем още един конкретен пример. Взимаме малка картинка със Супер Марио:

и ще я уголемяваме много. Ще сложим трите варианта един след друг:

Видимо е, че билинейната и бикубичната трансформация дават много подобни един на друг резултати. В конкретния случай е трудно да се прецени "кое е по-добро". Общите рецепти, които дават повечето хора в интернет, са в заключението по-долу.

Заключение

Използването на един или друг алгоритъм зависи от контекста на картинката, която ще се разширява. По принцип може да се следват следните правила:

1. Ако искаме да съхраним пикселизацията, използваме "най-близък съсед". Ако искаме "да се загладят ръбовете", използваме някой от другите два алгоритъма;
2. При уголемяване на картинка, може да се очаква билинейната интерполация да прави по-голямо замазване (повече blur), а бикубичната повече да изостря ръбовете (повече sharpness);
3. При намаляване на картинката (което става по същите алгоритми, но слабо засегнахме в конкретната статия) винаги има безвъзвратна загуба на качество. Счита се, че най-добрият алгоритъм за тези случаи е билинейния.