* Корекция на грешки с код на Хеминг
Публикувано на 04 септември 2017 в раздел Информатика.
Когато четем и записваме информация на хард диска на локалния компютър, рядко се замисляме "какво ще се случи ако стане проблем". Грешките се случват толкова рядко, че този проблем е пренебрежим. В някои езици за програмиране компилаторите ни принуждават да следим за Input/Output изключения при четенето на файлове, но това често ни се струва като досадно задължение. И все пак проблемът е фундаментален - имаме изпращане на информация от една точка в друга през комуникационен канал, но какво ще се случи ако има някаква грешка по време на преноса? Вече се досещате, че проблемът е често наличен при преноса на информация между два компютъра през мрежа, но може и да се изненадате, че същия проблем е наличен дори при комуникацията между централем процесор и рам памет!
Нека си измислим въображаем датчик, който отчита състоянието на някаква система и го предава на отдалечен източник във вид на следните съобщения: "работи нормално", "леко отклонение", "силно отклонение", "критично състояние". Едно от първите неща, които правим, е да измислим ефективен начин да пренасяме тези данни максимално компактно - да ги "компресираме". Можем да се досетим, че четири възможни съобщения могат да бъдат напълно определени от два бита, например по следния начин:
| Нормално | Леко | Силно | Критично |
00 01 10 11
Подобна компресия е максимална - по-добра не може да бъде постигната. Това не означава обаче, че тя е максимално ефективна - ако например в близо 100% от случаите ние изпращаме сигнал "Нормално", то бихме могли да направим неговия код от един единствен бит - например 0, - а останалите в трибитови комбинации, за да бъдат различими. Горното описание е максимално ефективно при равновероятностно (по 1/4) изпращане на всяко едно от състоянията. Тази тема няма да я разгледаме тук.
Въпросът, който си поставяме в тази статия, е "какво ще се случи ако един от битовете се промени поради грешка по време на преноса на данни"? В така изградената система е очевидно, че ако такова нещо се случи, ще пристигне погрешен сигнал. Целта ни е да изградим системата за пренос по такъв начин, че дори ако се промени бит, ние да можем да забележим, че това се е случило (error detection) и дори евентуално да го поправим (error correction).
Контролна сума
Една техника, която се използва изклюително често, е т.нар. "контролна сума". Това е поредица от битове, които се изчисляват по точно определен алгоритъм и ни позволяват да засечем кога има проблем със съобщението. Ако има промяна в подадената поредица, контролната сума ще бъде грешна и ще засечем, че има проблем. Аналогично ако има проблем при преноса на самата контролна сума, ние ще засечем, че има проблем при преноса, защото ще можем да я преизчислим и ще видим, че не съвпада с получената.
Да се върнем към първоначалния пример. Един възможен начин да въведем контролна сума е например да изберем контролен бит изключващо "или" между другите два предавани бита. XOR действа по следния начин: 0^0=0, 0^1=1^0=1, 1^1=0. Тоест вече можем да предаваме данните по следния начин:
| Нормално | Леко | Силно | Критично |
000 011 101 110
Представете си, че само един бит бъде сменен. Който и да е единствен бит, от която и да е избрана комбинация, ще направи така, че контролната сума няма да излиза коректно. Така еднозначно ще знаем, че има проблем в предадените данни. Проблемът е, че не знаем какъв точно е бил този проблем - не знаем кой точно бит е бил променен. Ако например сме получили 001, ние не знаем дали първоизточника е бил 101, 011 или 000 - всяко едно от тях е точно с един бит разлика от полученото.
Представете си 5-битов код, при който винаги имаме 3 нули и 2 единици. Твърдим, че с подобна комбинация е възможно да кодирате точно 10 възможни символа (например десетичните цифри от 0 до 9) така, че да имат контролна сума и да може да се засече еднобитова грешка при преноса на данни. Опитайте се да пресъсздадете този код и го проверете. Нарича се "код на Хеминг две-от-пет".
Сега нека се фокусираме върху проблема не със засичане на грешка, но и с нейното отстраняване. Един начин е да искаме "предаване наново" на данните, които сме видели, че са невалидни. Това е техника позната като "ACK и NAK" - след предаване на съобщение, получаващата страна трябва да върне потвърждение (ACK) ако всичко е било наред или сигнал за проблем (NAK) при несъвпадаща контролна сума. Съответно изпращача трябва да върне ACK ако е получил ACK или да препрати съобщението отново ако е получил NAK. Ако грешките се случват рядко, това е доста ефективен метод за комуникация (освен всичко друго той ни дава потвърждение, че ответната страна е получила данните, което обаче не е фокус на настоящата статия). Друга възможност е да вмъкнем вътре в самите съобщения допълнителни битове, с които да можем да разпознаем каква точно грешка се е получила и съответно да я поправим. Това ще бъде по-оптимално при наличие на шумен канал за комуникация.
Корекция на грешки
Нека опростим задачата и имаме само две възможни съобщения - 0 и 1. Нека добавим техните контролни суми, т.е. съобщенията стават 00 и 11. Видимо това не е достатъчно за да можем да определим при получаваме например на 01 какво е било оригиалното съобщение преди настъпването на грешката. Нека добавим още един контролен бит - засега ще го приемем просто като повторение на съобщението, т.е. ако съобщението е било 0, то повторено ще стане 00, а заедно с контролния бит и повторението ще стане 000, а ако е било 1, повторено ще бъде 11, а заедно с контролния бит ще стане 111. Твърдението ни е, че ако в предадено трибитово съобщение настъпи грешка при предаването на само един бит, ние ще можем не само да регистрираме грешката, но и да я поправим, тоест да коригираме грешката. Да проверим дали това е така.
Да речем, че сме получили 010. Такова съобщение е невалидно. Приемаме, че само един бит е бил променен при предаването на информация. Вероятно вече се досетихте кой точно бит е бил това - втория. Как се досетихте? Просто сравнявате полученото съобщение 010 с двете валидни - 000 и 111. За да получите 000 от 010 вие ще направите само една промяна - ще смените втория пит. За да получите 111 от 010 вие ще направите две промени - ще смените първия и третия бит. Тоест можем да кажем, че разстоянието между 010 и 000 е по-малко, отколкото разстоянието между 010 и 111. В такъв случай ще приемем, че оригиналното съобщение е било 000. Ако знаем, че само един бит е бил променен, тогава това е еднозначно вярно.
Можем много лесно да визуализираме съставената схема като вземем координатна система, на която нанесем куб със страна 1:
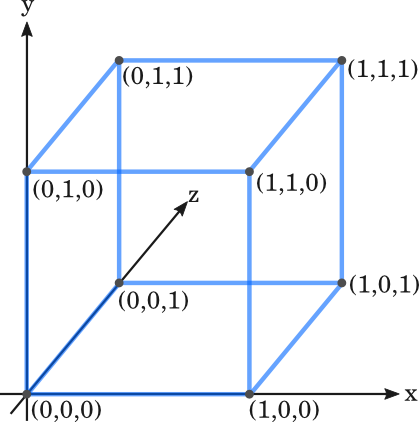
Двете валидни съобщения се намират на двата диаметрално противоположни върха на куба - 000 и 111. За да преминете от едното валидно състояние до другото, трябва да преминете през точно три ръба. Ще казваме, че това при това положение имаме дистанция 3. Всяко невалидно с 1 бит разлика съобщение ще попадне в един от другите възможни върхове на куба - 110, 101, 110, 010, 001 и 011. Вземете което и да е от невалидните състояния и поемете по най-краткия възможен път по ръбовете на куба по посока на валидно състояние. Ще видите, че винаги ще се намиране на един ръб разстояние от едното валидно състояние и на два ръба разстояние от другото.
Сега нека се върнем към оригиналната задача. При нея имахме четири съобщения - 00, 01, 10 и 11. Можем да приложим същата тактика - добавяне на оригиналното съобщение контролно втори път и добавяне на контролните битове, при това в този случай тази тактика ще работи. Тук обаче ще покажем една друга наредба с по-ефективно решение (не за конкретния случай, а при скалиране към по-големи съобщения), която е измислена през 1950 г. от Ричърд Хеминг:
- Битовете на съобщението се слагат на позиции 3 и 5. От петте възможни позиции, това са единствените, които не са числа, които са степени на двойката;
- Бит №1 ще действа като контролен за позиции 1, 3 и 5;
- Бит №2 ще действа като контролен за позиции 2 и 3;
- Бит №4 ще действа като контролен за позиции 4 и 5.
Нека го направим стъпка по стъпка. Първо ще поставим битовете на съобщенията:
| Бит 1 | Бит 2 | Бит 3 | Бит 4 | Бит 5 |
0 0
0 1
1 0
1 1
Сега да поставим първия контролен бит (Бит 1). Той ще действа като операция XOR от позиции 3 и 5. Понеже по-нагоре казахме, че е "контролен за позиции 1, 3 и 5", тук можем да интерпретираме това правило по следния начин - трябва така да подберем Бит 1, че ако преброим единиците на позиции 1, 3 и 5, трябва да се получи четен брой. Помислете и ще видите, че това отговаря точно на функция XOR.
| Бит 1 | Бит 2 | Бит 3 | Бит 4 | Бит 5 |
0 0 0
1 0 1
1 1 0
0 1 1
Сега да добавим Бит 2. При него ще приложим същия принцип. Казахме, че този бит отговаря за позиции 2 и 3, т.е. ще искаме на позиции 2 и 3 да има четен брой единици!
| Бит 1 | Бит 2 | Бит 3 | Бит 4 | Бит 5 |
0 0 0 0
1 0 0 1
1 1 1 0
0 1 1 1
Аналогично прилагаме правилото за Бит 5 - на позиции 4 и 5 трябва да има четен брой единици:
| Бит 1 | Бит 2 | Бит 3 | Бит 4 | Бит 5 |
0 0 0 0 0
1 0 0 1 1
1 1 1 0 0
0 1 1 1 1
Това са четирите възможни коректни съобщения, които съдържат 2 бита полезна информация и 3 контролни допълнителни бита. Твърдим, че при промяна на точно 1 бит, ние ще можем не само да засечем, че има грешка (проверете - няма единствен бит, който ако бъде сменен ще доведе до друго коректно съобщение), но и ще можем да намерим еднозначно кое е било оригиналното съобщение. Алгоритъмът за това е чрез последователна проверка на контролните битове. Направете няколко опита и проверете.
Подобен код ще наричаме [5, 2, 3] - пренасяме общо пет бита информация, в които има двубитово съобщение и валидните разстояния са на дистанция три едно от друго.
Дали не може да предадем 2 бита информация чрез 4 бита и да получим подобна корекция на грешки? Отговорът ще е отрицателен. Ако направите проекцията на четиримерен куб в тримерното пространство:

ще може да проверите сами, че няма да е възможно да изберете четири върха от външния и вътрешния куб така, че всички те да са на дистанция 3 един от друг.
Възможно ли е да направим по-голяма дистанция, с което да коригираме повече битове? Отговорът е положителен. Дори можем да изведем формула за това колко бита можем да коригираме спрямо дистанцията. Формулата е:
[math]\lfloor \frac{d-1}{2} \rfloor[/math]
където d e дистанцията, а странните скоби означават "закръгляване надолу". Например при дистанция 3 ще имаме възможност да коригираме 1 бит. При дистанция 4 отново ще можем да коригираме само 1 бит: (4-1)/2 = 3/2 = 1,5, което закръглено надолу е 1. При дистанция 5 вече ще можем да коригираме 2 бита. И т.н.
Как кодът на Хеминг ще се разширява по-нататък при по-дълги съобщения? Вече казахме, че информационните битове (носителите на полезна информация) ще са винаги на позиции, които не са степени на двойката, а контролните ще са на позиции степени на двойката. При това можем да определим еднозначно кой контролен бит за кои позиции отговаря по следната схема:
- Бит 1 ще отговаря за позиции 1, 3, 5, 7, 9, 11, ...;
- Бит 2 ще отговаря за позиции 2, 3, 6, 7, 10, 11, ...;
- Бит 4 ще отговаря за позиции 4, 5, 6, 7, 12, 13, 14, 15, ...;
- Бит 8 ще отговаря за позиции 8, 9, 10, 11, 12, 13, 14, 15, 24, 25, 26, 27, 28, 29, 30, 31, ...;
- Бит 16 ще отговаря за позиции 16, 17, ...;
Видяхте ли зависимостта? За всеки контролен бит на позиция 2n ще можем да кажем, че отговаря за n поредни бита от позиция n, след това пропуска n бита, след това пак отговаря за n поредни бита, пак пропуска n, и т.н. Опитайте се да изведете обща формула.
Остава да отговорим на въпроса дали сме постигнали оптималност? Отговорът при [5,2,3] е отрицателен, докато при междинния пример с куба, който можем да означим като [3,1,3] ще бъде положителен.
Причината да казваме, че [3,1,3] е оптимален е, че този код покрива всички възможни бинарни числа - той е оптимален откъм компактност. Действително нека видим двата възможни кода: 000 и 111. Сменяйки само един бит от първия код може да получите 100, 010 или 001. Сменяйки само един бит от втория код може да получите 011, 101 и 110. Значи имаме 2 валидни и 6 невалидни случая, което прави общо 8 възможни комбинации. Тоест това са всички възможни трибитови комбинации. Такъв код ще наричаме перфектен.
При кодът [5,2,3] може да се провери, че не е така. Имахме 4 валидни съобщения. Всяко едно от тях при смяна на 1 бит може да генерира по 5 невалидни. Тоест имаме общо 4 + 4*5 = 24 съобщения. Това по-малко от 32-те съобщения, които се покриват от 5-битово число. Именно затова казваме, че този код не е перфектен, т.е. не е оптимално компактен.
Кои са "перфектните" кодове и има ли формула за тях? Може би веднага ви стана ясно, че е свързано със степените на двойката. Следващите перфектни кодове ще са [7,4,3], [15,11,3], [31,26,3], [63,57,3], ... Успяхте ли да видите зависимостта? Общата формула е:
[math]\left[ 2^{r}-1, 2^{r}-r-1, 3 \right][/math]
Докажете, че така генерираните кодове ще са перфектни.
Перфектни кодове с други дължини
Досега основно се фокусирахме върху дължини 3, т.е. върху кодове, които коригират по един бит. Дали има перфектни кодове, които коригират повече битове? Един отговор например e [23, 12, 7] - това е един от "кодовете на Голей". Има и друг, но той не използва бинарна, а тринарна бройна система. Разглеждането на такива случаи ще е извън обхвата на тази статия.
Приложение
Освен при преноса на данни между комютри по мрежа и особено при пренасянето на данни чрез радиосигнал, изложената теория има приложение и в други сфери от практиката. Например можете да видите контролни суми при генерирането на ЕГН и при фабричните номера на двигателите на автомобилите (VIN). Така при преписване на номера от човек, софтуер може лесно да хване евентуална техническа грешка. Корекцията на грешки пък се използва при ECC оперативната памет на компютрите - това са по-скъпи RAM памети, които се използват при сървъри.
Добави коментар