C, PHP, VB, .NET

Продължаваме още малко с комплексните числа. Както вече знаем, всяко комплесно число „z“ може да се представи в алгебричен вид като z=a+bi, където „a“ наричахме „реална част“, а „b“ наричахме „имагенерна част“. Нека направим координатна система, в която по оста „x“ ще нанасяме реалните части, а по оста „y“ имагенерните части на комплексните числа. По този начин всяка точка от тази координатна система ще представя точно определено комплексно число:

 

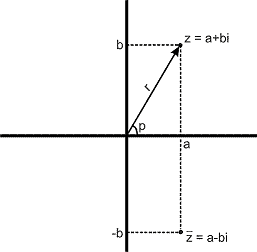
Вижда се ясно, че комплекно-спрегнатото число на дадено комплексно число отговаря на точка, която е симетрична спрямо реалната ос.

Дължината на вектора с начало т.(0,0) и край точката (a,b) ще означаваме с „r“ и ще наричаме „радиус-вектор“ или „модул“ на комплекното число. Лесно чрез Питагоровата теорема можете да намерите, че:

[math]r = |z| = \sqrt{a^2+b^2}[/math]

Ако „p“ е ъгъла, който сключва радиус-вектора „r“ с реалната ос „x“, то може изчислим координатите на точката по следния начин:

[math]a = r.cosp\\b = r.sinp[/math]

Следователно ще можем да записваме комплекното число „z“ по следния начин:

[math]z = r.cosp + r.i.sinp = r(cosp + i.sinp)[/math]

Записани по този начин координатите на комплексното число се наричат „полярни“, а самия начин на записване ще наричаме „тригонометричен вид“ на комплекното число.

Знаем, че sin и cos са периодични функции с период от 2π. Затова ще дефинираме ъгъла „p“ по следния начин:

[math]p = Arg(z)\\ p_0 = arg(z)\\ Arg(z)=arg(z)+2k\pi, k=0,\pm1,\pm2,…[/math]

Arg(z) ще наричаме „аргумент“ на комплексното число, а arg(z) – главна стойност на аргумента.

Твърдение: Две комплексни числа са равни тогава и само тогава, когато модулите им са равни, а аргументите им се различават с кратно на 2π число.

Задача 1. Представете числото z=2+2i в тригонометричен вид

Решение: Първо намираме модула:

[math]r = |z| = \sqrt{2^2+2^2} = \sqrt{8} = 2\sqrt{2}[/math]

Сега ще намерим аргумента от следната система:

[math]\left|\begin{array}{l}cosp = \frac{a}{|r|} = \frac{2}{2\sqrt{2}}=\frac{1}{\sqrt{2}} \\\\ sinp=\frac{b}{|r|} = \frac{2}{2\sqrt{2}}=\frac{1}{\sqrt{2}} \end{array}\right.[/math]

От тази система можем да намерим ъгъл p:

[math]p = \frac{\pi}{4}+2k\pi[/math]

от където и самото комплексно число:

[math]z = 2\sqrt{2}.(cos(\frac{\pi}{4}+2k\pi) + i.sin(\frac{\pi}{4}+2k\pi))[/math]

Задача 2. Представете комплексното число z=3 в тригонометричен вид

Решение: Намираме модула:

[math]r = |z| = \sqrt{3^2 + 0^2} = 3[/math]

След което аргументите:

[math]\left|\begin{array}{l}cosp = \frac{a}{|r|} = \frac{3}{3}=1 \\\\ sinp=\frac{b}{|r|} = \frac{0}{3}=0 \end{array}\right.[/math]

=> p = 0+2kπ

=> z = 3.(cos(2kπ)+i.sin(2kπ))

Задача 3. Представете числото [mathi]z=-\sqrt{3}+i[/mathi] в тригонометричен вид

Решение: Първо намираме модула:

[math]r = |z| = \sqrt{(-\sqrt{3})^2+1^2}=\sqrt{4} = 2[/math]

След което аргументите:

[math]\left|\begin{array}{l}cosp = \frac{a}{|r|} = \frac{-\sqrt{3}}{2} \\\\ sinp=\frac{b}{|r|} = \frac{1}{2}\end{array}\right.[/math]

=> [mathi]p = \frac{5\pi}{6}+2k\pi[/mathi]

=> [mathi]z=2.(cos(\frac{5\pi}{6}+2k\pi)+i.sin(\frac{5\pi}{6}+2k\pi))[/mathi]

Умножение на комплексни числа в тригонометричен вид: Нека [mathi]z_1 = r_1(cosp_1 + i.sinp_1)[/mathi] и [mathi]z_2 = r_2(cosp_2 + i.sinp_2)[/mathi]. Намерете произведението [mathi]z=z_1.z_2[/mathi]

Решение: Разкриваме скобите:

[math]z=z_1.z_2 = r_1(cosp_1 + i.sinp_1).r_2(cosp_2 + i.sinp_2)[/math]

=>

[math]z=r_1r_2(cosp_1cosp_1+isinp_2cosp_1+isinp_1cosp_2+i^2sinp_1sinp_2)[/math]

=>

[math]z=r_1r_2(cosp_1cosp_2-sinp_1sinp_2 + i(sinp_2cosp_1+sinp_1cosp_2))[/math]

Вътре в скобите имаме добре познати формули от тригонометрията, =>

[math]z = r_1r_2(cos(p_1+p_2)+ i.sin(p_1+p_2))[/math]

=> при умножение модулите се умножават, а аргументите се събират.

Деление на комплексни числа в тригонометричен вид: Аналогично можете лесно да докажете, че

[math]\frac{z_1}{z_2} = \frac{r_1}{r_2}(cos(p_1-p_2)+ i.sin(p_1-p_2))[/math]

=> при деление модулите се делят, а аргументите се изваждат.

Формула на Моавър: Ще я дадем без доказателство. Формулата на Моавър гласи, че:

[math]z^n = r^n(cos(np+2k\pi)+i.sin(np+2k\pi))[/math]

Формулата важи и за отрицателни и за дробни числа.

Задача 4. Изчислете

[math]z = \frac{(1+i)^5}{(1-i)^3}[/math]

Решение: Първо представяме комплексните числа в скобите от числителя и знаменателя в тригонометричен вид:

[math]z_1=1+i=>z_1 = \sqrt{2}.(cos(\frac{\pi}{4})+i.sin(\frac{\pi}{4}))[/math]

и

[math]z_2=1-i=>z_2 = \sqrt{2}.(cos(-\frac{\pi}{4})+i.sin(-\frac{\pi}{4}))[/math]

=>

[math]z = \frac{(\sqrt{2}.(cos(\frac{\pi}{4})+i.sin(\frac{\pi}{4})))^5}{(\sqrt{2}.(cos(-\frac{\pi}{4})+i.sin(-\frac{\pi}{4})))^3}[/math]

Прилагаме формулата на Моавър:

[math]z=\frac{\sqrt{2}^5}{\sqrt{2}^3}.\left(\frac{(cos\frac{5\pi}{4}+isin\frac{5\pi}{4})}{(cos\frac{-3\pi}{4}+isin\frac{-3\pi}{4})} \right )[/math]

Две комплексни числа в тригонометричен вид се делят като разделим модулите им и извадим аргументите им:

[math]z = 2.(cos(2\pi+2k\pi)+isin(2\pi+2k\pi))[/math]

(добавихме и периода 2kπ)

=> z=2

Задача 5. Намерете

[math]\left(\frac{1+i}{\sqrt{2}} \right)^{100}[/math]

Решение: Числото вътре в скобите е:

[math]\frac{1}{\sqrt{2}} + i.\frac{1}{\sqrt{2}}[/math]

Трябва да го превърнете в тригонометричен вид. От там намирате:

[math]z = \left(1.(cos\frac{\pi}{4}+i.sin\frac{\pi}{4})\right)^{100}[/math]

Прилагаме формулата на Моавър

[math]z=cos(25\pi+2k\pi) + i sin(25\pi+2k\pi)[/math]

Задача 6. Намерете

[math]z = \left(\frac{\sqrt{3}+5i}{4+2\sqrt{3}i} \right )^{66}[/math]

Решение: Един начин е да представите числителя и знаменателя като числа в тригонометричен вид, след което да ги разделите и накрая да приложите формулата на Моавър.

Друг начин е първо да опростим израза вътре в скобите, да представим полученото число в тригонометричен вид и накрая да приложим формулата на Моавър. Ще решим задачата по този начин:

[math]z=\left(\frac{(\sqrt{3}+5i)(4-2\sqrt{3}i)}{(4+2\sqrt{3}i)(4-2\sqrt{3}i)}\right)^{66}= \left(\frac{(4\sqrt{3}-6i+20i-10\sqrt{3}i^2)}{16+12}\right)^{66}=\left(\frac{\sqrt{3}}{2}+\frac{1}{2}i\right)^{66}[/math]

Представяме числото вътре в скобите в тригонометричен вид:

[math]z = \left(cos\frac{\pi}{6}+isin\frac{\pi}{6} \right)^{66} = cos(11\pi+2k\pi)+isin(11\pi+2k\pi) = -1[/math]